8 Regresija
Zanima nas modeliranje slučajne varijable \(Y\) na temelju \(p\geq 1\) slučajnih varijabli (prediktora) \(X_1, \dots, X_p\) . U slučaju \(p=1\) govorimo o jednostavnoj regresiji. Pri tome raspolažemo podacima u \(n\) mjerenja
\[(y_1, \mathbb{x}_1), \dots, (y_n, \mathbb{x}_n),\] pri čemu je \(\mathbb{x}_i=\left(x_{i,1}, \dots, x_{i,p}\right), \quad x_{i,j} \in \mathbb{R},\, i \in \{1, \dots, n\}, j \in \{1, \dots p\}.\)
Regresijski model je općenito oblika
\[Y_i=f(\mathbb{x}_i) + \epsilon_i, \, i=1, \dots, n\, (\text{ regresijski model })\] gdje su \(\epsilon_1, \dots, \epsilon_n\) slučajne varijable takve da je \(E\epsilon_i=0, \, i \in \{1, \dots, n\}\) koje zovemo greške.
Obično koristimo dodatne pretpostavke na greške u svrhu modelskog zaključivanja. S druge strane, oblik funkcije \(f\) definira tip regresije (linearna, eksponencijalna regresija…).
Primijetimo da regresijski model možemo zapisati i u alternativnom obliku
\[E[Y_i | \mathbb{X}_i= \mathbb{x}_i] =f(\mathbb{x}_i), \, i \in \{1, \dots, n\}.\] Umjesto očekivanja, moguće je modelirati neku njegovu funkciju (koju zovemu funkcija veze, eng. link function), a tada govorimo o generaliziranim regresijama, od kojih izdvajamo generalizirane linearne modele (GLM) koji podrazumijevaju linearan izbor funkcije \(f\). Svi modeli koje ćemo obraditi su specijali slučajevi GLM modela.
8.1 Linearna regresija
Linearna regresija je specijalni slučaj GLM metoda kod kojih izravno modeliramo očekivanje kao linearnu kombinaciju prediktora, tj. za funkciju \(f\) biramo \[f(\mathbb{x}_i)=\mathbb{\beta}^T \mathbb{x_i}= \beta_1 x_{i,1} + \beta_2 x_{i,2} + \dots \beta_p x_{i,p}.\] U Bayesovskoj paradigmi parametar \(\mathbb{\beta}\) je slučajna varijabla, a u tom kontekstu nas zanima distribucija \(f(y | \mathbb{x})\). Linearna regresija podrazumijeva linearan oblik distribucije \(f(y | \mathbb{x})\), tj. \[\int y f(y | \mathbb{x}) dy = E[Y | \mathbb{x}]= \beta_1 x_{1} + \beta_2 x_{2} + \dots \beta_p x_{p}=\mathbb{\beta}^T \mathbb{x}.\] Međutim, radi potpunosti Bayesovskog modela potrebno je specifizirati vjerodostojnost, a ne samo jednu numeričku karakteristiku. U tu svrhu koristimo pretpostavku o normalnosti i nezavisnosti grešaka: \[(\epsilon_1, \dots, \epsilon_n) \text{ j.s.u. iz } \mathcal{N}(0, \sigma^2).\] Time je vjerodostojnost zadana s
\[\begin{align*} f(y_1, \dots, y_n | \mathbb{x}_1, \dots, \mathbb{x}_n, \mathbb{\beta}, \sigma^2)&=\prod_{i=1}^{n}f(y_i | \mathbb{x}_i, \mathbb{\beta}, \sigma^2 ) \\ &= \frac{1}{\sqrt{(2\pi\sigma^2)^n}}exp\{-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(y_i - \mathbb{\beta} \mathbb{x}_i)^2\} \end{align*}\]
Prepostaje definirati apriorne distribucije za \(\mathbb{\beta}\) i \(\sigma^2\) kako bi Bayesovski model bio potpun.
U frekvencionističkoj linearnoj regresiji \(\mathbb{\beta}\) i \(\sigma^2\) su fiksne veličine, a vjerodostojnost će biti maksimizirana kada je suma kvadrata reziduala \(SSR(\mathbb{\beta}))=\sum_{i=1}^{n}(y_i - \mathbb{\beta}^T \mathbb{x}_i)^2\) minimizirana. Pokazuje se da je MLE procjenitelj \[\hat{\beta}_{OLS}=\left(\mathbb{X}^T \mathbb{X}\right)^{-1} \mathbb{X}^T \mathbb{y}.\]
Definiranu vjerodostojnosti možemo zapisati i u multivarijatnom obliku, tj. imamo \[\{\mathbb{Y} | \mathbb{X}, \mathbb{\beta}, \sigma^2\} \sim \mathcal{N}(\mathbb{X}\mathbb{\beta}, \sigma^2 \mathbb{I})\]
Ovaj Bayesovski model dopušta semikonjugate:
\[\begin{align*} \mathbb{\beta} \sim \mathcal{N}(\mathbb{\beta}_0, \Sigma_0) &\Rightarrow \{\mathbb{\beta} | \mathbb{Y}=\mathbb{y}, \mathbb{X}=\mathbb{x}, \sigma^2\} \sim \mathcal{N}\left((\Sigma^{-1}_0+\mathbb{X}^T\mathbb{X}/\sigma^2)^{-1}(\Sigma^{-1}_0 \mathbb{\beta}_0 + \mathbb{X}^T \mathbb{y}/\sigma^2), (\Sigma^{-1}_0+\mathbb{X}^T\mathbb{X}/\sigma^2)^{-1})\right) \\ 1/\sigma^2 \sim \Gamma(\nu_0/2, \nu_0 \sigma^2_0/2) &\Rightarrow \{\sigma^2 | \mathbb{Y}=\mathbb{y}, \mathbb{X}=\mathbb{x}, \mathbb{\beta}\} \sim InvGama\left(\frac{\nu_0+n}{2}, \frac{\nu_0 \sigma^2_0 + SSR(\mathbb{\beta})}{2}\right). \end{align*}\]
Na temelju ovih semikonjugata moguće je napraviti posteriornu aproksimaciju koristeći Gibbsovo uzorkovanje.
Radi usporedbe s frekvencionistički procjeniteljem uočimo:
\[E\left[\mathbb{\beta} | \mathbb{Y}=\mathbb{y}, \mathbb{X}=\mathbb{x}, \sigma^2\right] \approx (\mathbb{X}^T \mathbb{X})^{-1} \mathbb{X} \mathbb{y} = \hat{\beta}_{OLS}\] ako je \(\Sigma^{-1}_0\) matrica male magnitude.
S druge strane, mogu se koristiti i slabo informativne apriorne distribucije, od kojih izdvajamo popularnu “g-apriornu distribuciju” koja osigurava da je procjena parametara invarijantna s obzirom na skalu regresora (primjerice jesu li podaci iskazani na mjesečnoj ili godišnjoj razini). Osim toga omogućuje da koristimo izravno MC metodu, umjesto korelirane MCMC metode:
\[\begin{align*} \mathbb{\beta} \sim \mathcal{N}\left(\mathbb{0}, g \sigma^2 \left(\mathbb{X}^T \mathbb{X}\right)^{-1}\right) &\Rightarrow \{\mathbb{\beta} | \mathbb{Y}=\mathbb{y}, \mathbb{X}=\mathbb{x}, \sigma^2\} \sim \mathcal{N}\left(\frac{g}{g+1}(\mathbb{X}^T \mathbb{X})^{-1} \mathbb{X} \mathbb{y}, \frac{g}{g+1} \sigma^2 (\mathbb{X}^T \mathbb{X})^{-1}\right) \\ 1/\sigma^2 \sim \Gamma(\nu_0/2, \nu_0 \sigma^2_0/2) &\Rightarrow \{\sigma^2 | \mathbb{Y}=\mathbb{y}, \mathbb{X}=\mathbb{x}\} \sim InvGama\left(\frac{\nu_0+n}{2}, \frac{\nu_0 \sigma^2_0 + SSR_g}{2}\right). \end{align*}\]
8.1.1 O selekciji modela u linearnoj regresiji
Ukoliko imamo velik broj mogućih prediktora na raspolaganju potrebno je odabrati razuman broj kvalitetnih prediktora za model. U Bayesovskoj paradigmi selekcija modela (u modelu linearne regresije koje prediktore uključiti) je jednostavna. Definiramo niz Bernoullijevih slučajnih varijabli kojim omogućujemo uključivanje/isključivanje pojedinog prediktora:
\[Y_i=z_1 b_1 x_{i,1} + \dots z_p b_p x_{i, p} + \epsilon_i,\] gdje je \[\beta_j=z_j \cdot b_j, \quad z_j \in \{0,1\}, \, b_j \in \mathbb{R}.\] Uvođenjem \(\mathbb{z}=(z_1, \dots, z_p)\) možemo uspoređivati modele s različitim prediktora na temelju Bayesovog faktora:
\[BF=\frac{P(\mathbb{y} | \mathbb{X}=\mathbb{x}, z_{a})}{P(\mathbb{y} | \mathbb{X}=\mathbb{x}, z_{b})}=\frac{P(z_{a} | \mathbb{y}, \mathbb{X}=\mathbb{x})}{P(z_{b} | \mathbb{y}, \mathbb{X}=\mathbb{x})} \cdot \frac{P(z_a)}{P(z_b)},\] pri čemu nizovi nula i jedinica \(z_a\) i \(z_b\) specifiziraju koji su prediktori uključeni u dva različita modela (a i b).
Treba napomenuti kako nam je sada potrebna posteriorna distribucija \(f(z | \mathbb{y}, \mathbb{x})\) kako bismo mogli računati pripadni BF.
Analogno bismo napravili i za proizvoljnu regresiju.
8.2 Poissonova regresija
Raspolažemo podacima u \(n\) mjerenja
\[(y_1, \mathbb{x}_1), \dots, (y_n, \mathbb{x}_n), \quad y_i \in \mathbb{N}_0,\] pri čemu je \(\mathbb{x}_i=\left(x_{i,1}, \dots, x_{i,p}\right), \quad x_{i,j} \in \mathbb{R},\, i \in \{1, \dots, n\}, j \in \{1, \dots p\}.\)
Poissonova regresija podrazumijeva sljedeću strukturu:
\[\begin{align*} & Y_i | \beta_0, \dots, \beta_p \sim \mathcal{P}(\lambda_i), \quad \lambda_i>0, \,\beta_k \in \mathbb{R}, \, i \in \{1, \dots, n\}, k \in \{1, \dots p\} \\ & \ln{(\lambda_i)}=\beta_0 + \beta_1 x_{i,1}+ \dots \beta_p x_{i,p},\quad i \in \{1, \dots, n\}. \end{align*}\]
Interpretacija parametara:
- \(\beta_0\): kada su \(X_{i,1}=X_{i,2}= \cdots X_{i, p}=0\) tada je očekivana vrijednost od \(Y_i\) jednaka \(e^{\beta_0}\)
- \(\beta_k\): Neka je \(\lambda_k\) očekivana vrijednost od \(Y_i\) kada je \(X_{i,k}=x\) (uz ostale prediktore fiksne). Ako \(X_{i, k}\) povećamo za jediničnu vrijednost (iz \(x\) u \(x+1\)) imamo \[\beta_k=\ln{(\lambda_{x+1})-\ln{(\lambda_x)}}, \quad e^{\beta_k}= \frac{\lambda_{x+1}}{\lambda_x}.\] Dakle, \(e^{\beta_k}\) je multiplikativna promjena u očekivanoj vrijednosti \(Y_i\) (\(\beta_k\) je promjena u logaritmiranoj očekivanoj vrijednosti \(Y_i\)).
S druge strane, usporedimo linearnu i Poissonovu regresiju:
- Za razliku od linearne regresije ovdje nemamo “greške” (\(\epsilon_i\)) u modelu jer Poissonova distribucija ima ugrađenu varijancu kroz očekivanje (\(EY=Var(Y)=\lambda\)).
- Za razliku od linearne regresiji ovdje ne modeliramo izravno uvjetno očekivanje \(E[Y_i | \mathbb{X}_i=\mathbb{x}_i]\) već njegovu logaritamsku transformaciju. Dakle u Poissonovoj regresiji funkcija veze je logaritamska funkcija, dok je u linearnoj regresiji identiteta.
- Linearna regresija podrazumijeva normalan model za podatke, dok Poissonova regresija Poissonov model za podatke
Prema tome i Poissonova regresija spada u GLM metode. U ovoj vrsti regresije nema jednostavnih semikonjugata koji vode prema posteriornoj distribuciju koja je poznata u zatvorenom obliku. U tom slučaju najjednostavnije je koristiti normalne apriorne distribucije za parametre budući da \(\ln{(\lambda_i)}\) može biti bilo koji realan broj.
- Struktura podataka : uvjetno na prediktore \(\mathbb{X}_i\), \(Y_i\) je nezavisan od ostalih mjerenja \(Y_j\).
- Struktura (zavisne) varijable \(Y\): \(Y\) ima Poissonovu distribuciju i predstavlja diskretan brojač događaja unutar fiksnog intervala vremena ili prostora.
- Struktura veze: logaritmirana očekivana vrijednost od \(Y\) može se zapisati kao linearna kombinacija prediktora (\(\ln{(\lambda_i)}=\beta_0+ \beta_1 x_{i,1}+ \dots \beta_p x_{i, p}\)).
- Struktura varijabilnosti u \(Y\): \(EY=Var Y=\lambda \Rightarrow\) uvjetno na prediktore \(\mathbb{X}\), tipična vrijednost od \(Y\) bi trebala približno biti jednaka varijabilnosti u \(Y\) (varijabilnost raste s očekivanjem).
8.3 Logistička regresija
Logističku regresiju koristimo kada želimo raditi binarnu klasifikaciju na temelju prediktora. Raspolažemo podacima u \(n\) mjerenja
\[(y_1, \mathbb{x}_1), \dots, (y_n, \mathbb{x}_n), \quad y_i \in \{0,1\},\] pri čemu je \(\mathbb{x}_i=\left(x_{i,1}, \dots, x_{i,p}\right), \quad x_{i,j} \in \mathbb{R},\, i \in \{1, \dots, n\}, j \in \{1, \dots p\}.\)
Logistička regresija podrazumijeva sljedeću strukturu:
\[\begin{align*} & Y_i | \beta_0, \dots, \beta_p \sim Ber(\pi_i), \quad \pi_i \in \langle 0, 1\rangle, \,\beta_k \in \mathbb{R}, \, i \in \{1, \dots, n\}, k \in \{1, \dots p\} \\ & \ln{\left(\frac{\pi_i}{1-\pi}\right)}=\beta_0 + \beta_1 x_{i,1}+ \dots \beta_p x_{i,p},\quad i \in \{1, \dots, n\}. \end{align*}\]
Interpretacija parametara:
- \(\beta_0\): kada su \(X_{i,1}=X_{i,2}= \cdots X_{i, p}=0\) tada šanse za događaj uspjeha (1) \(e^{\beta_0}\)
- \(\beta_k\): Ukoliko sve prediktore osim \(X_{i, k}\) držimo fiksnim i \(X_{i, k}\) poraste za jediničnu veličinu (iz \(x\) u \(x+1\)) imamo: \[\beta_k=\ln{(\text{šanse}_{x+1})-\ln{(\text{šanse}_x)}}, \quad e^{\beta_k}= \frac{\text{šanse}_{x+1}}{\text{šanse}_x}.\]
Niti u ovom modelu nećemo proučavati semikonjugate, a za apriorne distribucije parametara možemo koristiti normalnu distribuciju koja reflektira naše subjektivno znanje o problemu (kroz interpretaciju parametara).
Uočimo kako je u ovom modelu funkcija veze logistička funkcija \(logit(x)=\ln{\left(\frac{x}{1-x}\right)}\) jer je \(\pi_i=E[Y_i | \mathbb{X}_i=\mathbb{x}_i]\).
8.3.1 Klasifikacija u logističkom modelu
Napravimo MCMC simulaciju \(N\) prediktivnih vrijednosti modela \(\{\tilde{Y}_1, \dots \tilde{Y}_N\}\) i izračunamo proporciju uspjeha (1) u simuliranim vrijednostima u oznaci p.
Ukoliko postavimo klasifikacijski “cut-off” \(c \in \left[0,1 \right]\) imamo:
- Ako je \(p \geq c\) klasificiraj \(Y\) kao 1.
- Ako je \(p < c\) klasificiraj \(Y\) kao 0.
“Cut off” \(c\) subjektivno zadajemo i ovisi o problematici.
8.4 Zadaci
Zadatak 8.1 U bazi podataka bikes nalaze se podaci o korisnicima usluge dijeljenog korištenja bicikla u Washingtonu.
- Promotrite podatke o broju vožnji bicikala po danu. Predložite distribucijski model za podatke.
- Predložite i implementirajte model za broj vožnji bicikala po danu u ovisnosti o temperaturi koristeći STAN platformu. Prilikom definiranja apriornih distribucija koristite sljedeće informacije:
- Na tipični dan (s temperaturom 70 \(F\)) očekujemo \(5000\) vožnji, a uzevši u obzir varijabilnost, očekujemo između \(3000\) i \(7000\) vožnji.
- Za svako povećanje temperature u iznosu 1 stupanj, broj vožnji se tipično poveća za 100, a ako uzmemo u obzir neizvjesnost očekujemo povećanje između 20 i 180.
- Za proizvoljnu temperaturu, broj dnevnih vožnji varira s tipičnom standardnom devijacijom od 1250 vožnji.
- Interpertirajte posteriorne distribucije regresijskih parametara \(\beta_0\) i \(\sigma\).
- Aproksimirajte posteriornu prediktivnu distribuciju broja vožnji bicikala na slučajno odabrani dan s temperaturom \(75\) \(F\).
- Aproksimirajte posteriornu vjerojatnost da na slučajno odabrani dan s temperaturom od 75 \(F\) broj vožnji bicikala bude između 2500 i 5000.
- Ukoliko se temperatura poveća za 1 stupanj, koliku promjenu u očekivanom broju vožnji očekujete?
model.bicikli <- "
data {
int<lower = 0> n;
vector[n] Y;
vector[n] X;
}
parameters {
real beta0;
real beta1;
real<lower = 0> sigma;
}
model {
Y ~ normal(beta0 + beta1 * X, sigma);
beta0 ~ normal(-2000, 1000);
beta1 ~ normal(100, 40);
sigma ~ exponential(0.0008);
}
generated quantities {
real y_tilda = normal_rng(beta0 + beta1 * 75, sigma);
}
"
model.bicikli.sim <-
stan(model_code = model.bicikli,
data = list(n = nrow(bikes), Y = bikes$rides, X = bikes$temp_feel),
chains = 4, iter = 5000*2, cores=1, refresh=0, seed = 84735)
print(model.bicikli.sim)Inference for Stan model: anon_model.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5%
beta0 -2170.44 3.96 329.75 -2817.70 -2392.27 -2172.94 -1944.64 -1534.26
beta1 81.76 0.06 4.72 72.62 78.56 81.79 84.93 90.93
sigma 1283.40 0.44 41.18 1205.40 1254.96 1282.20 1310.99 1366.71
y_tilda 3962.69 9.08 1287.78 1426.45 3102.41 3960.33 4829.04 6504.58
lp__ -3822.26 0.01 1.18 -3825.29 -3822.81 -3821.96 -3821.39 -3820.89
n_eff Rhat
beta0 6923 1
beta1 6927 1
sigma 8748 1
y_tilda 20125 1
lp__ 6610 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:50:59 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).- Posteriorne distribucije parametara treba uspoređivati s početnim apriornim uvjerenjem koje smo postavili u modelu. Tako primjerice, za \(\beta_0\) nakon što vidimo podatke na tipičan dan očekujemo ipak nešto manje vožnji, to jest približno 4830 vožnji, odnosno uzmemo li u obzir neizvjesnost očekujemo između 4183 i 5466 vožnji. Dakle, nakon što vidimo podatke očekujemo manje vožnji, ali uz manju neizvjesnost.
S druge strane za \(\sigma\): očekujemo nešto veću varijabilnost u broju vožnji na proizvoljan dan (\(1283\)), uz \(0.05\)-vjerodostojni interval \(\left[1205.4, 1366.71\right]\).
mcmc_dens(model.bicikli.sim, pars="beta0")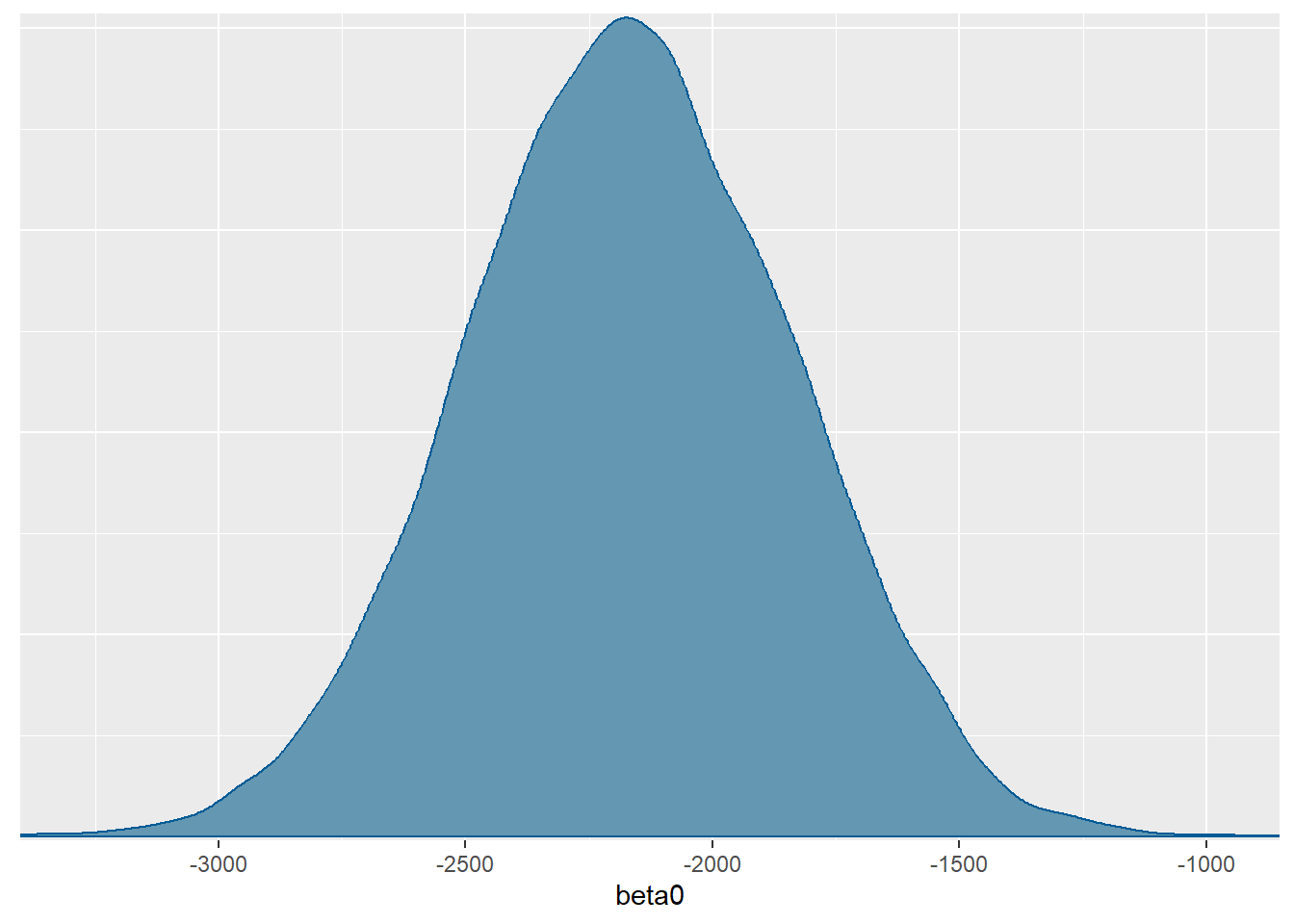
mcmc_dens(model.bicikli.sim, pars="sigma")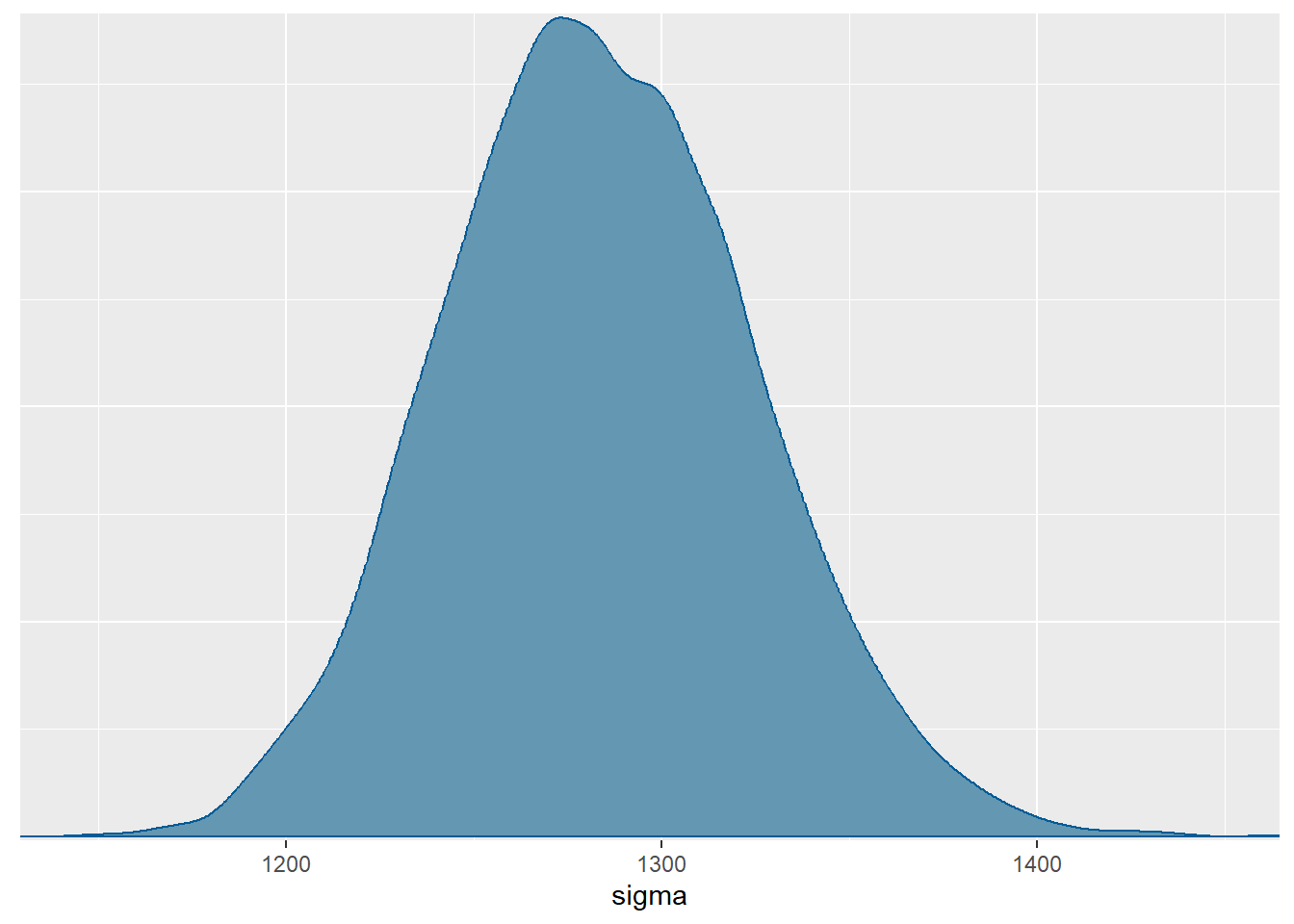
mcmc_dens(model.bicikli.sim, pars="y_tilda")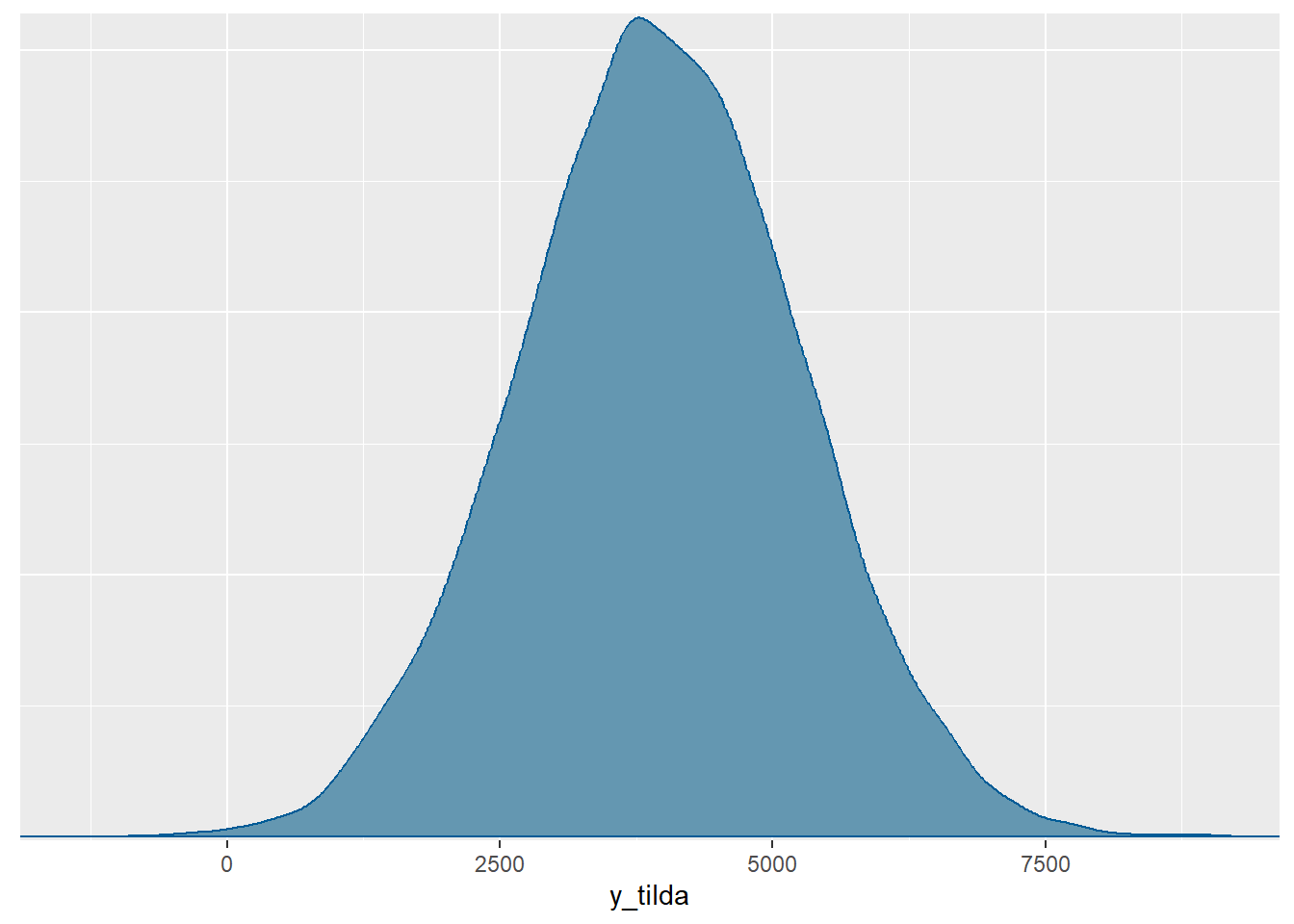
MCMC.bicikli <- rstan:: extract(model.bicikli.sim)
ecdf(MCMC.bicikli$y_tilda)(5000)-ecdf(MCMC.bicikli$y_tilda)(2500)[1] 0.66195- Odgovor nam daje parametar \(\beta_1\), odnosno pripadna posteriorna distribucija. Prema modelu, očekujemo povećanje između \(73\) i \(91\) vožnji s \(95\%\) vjerojatnosti. Uzmemo li u obzir posteriorno očekivanje parametra \(\beta_1\), možemo reći da prema modelu očekujemo približno \(82\) nove vožnje za svako jedinično povećanje temperature.
mcmc_dens(model.bicikli.sim, pars="beta1")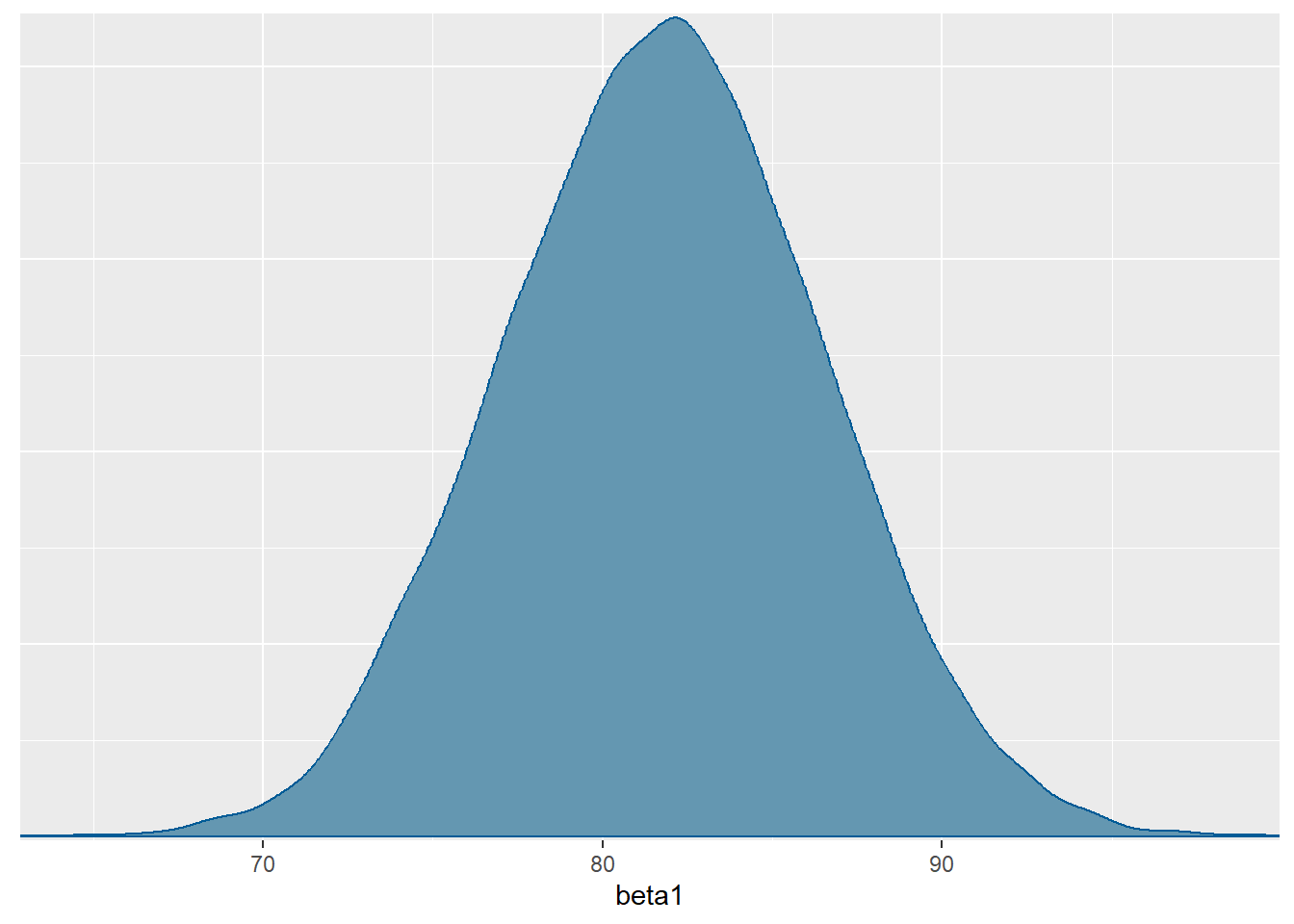
Zadatak 8.2 U bazi podataka airbnb_small nalaze se podaci o smještaju izlistanom na platformi Airbnb u Chicagu iz 2016. godine.
- Promotrite podatke o broju recenzija po smještaju. Predložite distribucijski model za podatke.
- Predložite i implementirajte model za broj recenzija po smještaju u ovisnosti o ocjeni smještaja koristeći STAN platformu. Prilikom definiranja apriornih distribucija koristite sljedeće informacije:
- Za tipični novi smještaj očekujemo 10 recenzija, a uzevši u obzir varijabilnost, očekujemo između \(5\) i \(15\) recenzija.
- Za svako povećanje ocjene smještaja u jediničnom iznosu, broj recenzija se multiplikativno poveća za 0.5, a ako uzmemo u obzir neizvjesnost očekujemo multiplikativno povećanje između 0.1 i 0.9.
- Interpertirajtu posteriornu distribuciju regresijskog parametra \(\beta_0\).
- Aproksimirajte posteriornu prediktivnu distribuciju broja recenzija po smještaju za slučajno odabrani smještaj ocjenom \(5\).
- Aproksimirajte posteriornu vjerojatnost da za slučajno odabrani smještaj s ocjenom \(5\) broj pripadnih recenzija bude veći od 30.
- Ukoliko se ocjena smještaja poveća za 0.5, koliku promjenu u očekivanom broju recenzija smještaja očekujete?
model.airbnb <- "
data {
int<lower = 0> n;
array[n] int Y;
vector[n] X;
}
parameters {
real beta0;
real beta1;
}
model {
Y ~ poisson(exp(beta0 + beta1 * X));
beta0 ~ normal(2.3, 0.9);
beta1 ~ normal(-0.7, 2.56);
}
generated quantities {
real y_tilda = poisson_rng(exp(beta0 + beta1 * 5));
}
"
model.airbnb.sim <-
stan(model_code = model.airbnb,
data = list(n = nrow(airbnb_small), Y = airbnb_small$reviews, X = airbnb_small$rating),
chains = 4, iter = 5000*2, cores=1, refresh=0, seed = 934)
print(model.airbnb.sim)Inference for Stan model: anon_model.
4 chains, each with iter=10000; warmup=5000; thin=1;
post-warmup draws per chain=5000, total post-warmup draws=20000.
mean se_mean sd 2.5% 25% 50% 75% 97.5%
beta0 2.00 0.00 0.11 1.78 1.92 2.00 2.07 2.21
beta1 0.27 0.00 0.02 0.23 0.26 0.27 0.29 0.32
y_tilda 28.70 0.04 5.34 19.00 25.00 29.00 32.00 40.00
lp__ 54687.25 0.01 0.97 54684.64 54686.87 54687.54 54687.95 54688.20
n_eff Rhat
beta0 2599 1
beta1 2599 1
y_tilda 19754 1
lp__ 4159 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:53:45 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).- Posteriornu distribucije parametra \(\beta_0\) treba uspoređivati s početnim apriornim uvjerenjem koje smo postavili u modelu. Tako primjerice, za \(\beta_0\) nakon što vidimo podatke za tipičan novi smještaj očekujemo ipak nešto manje recenzija, to jest približno 7 recenzija, odnosno uzmemo li u obzir neizvjesnost očekujemo između 6 i 9 recenzija. Dakle, nakon što vidimo podatke očekujemo manje recenzija, ali uz manju neizvjesnost.
mcmc_dens(model.airbnb.sim, pars="beta0")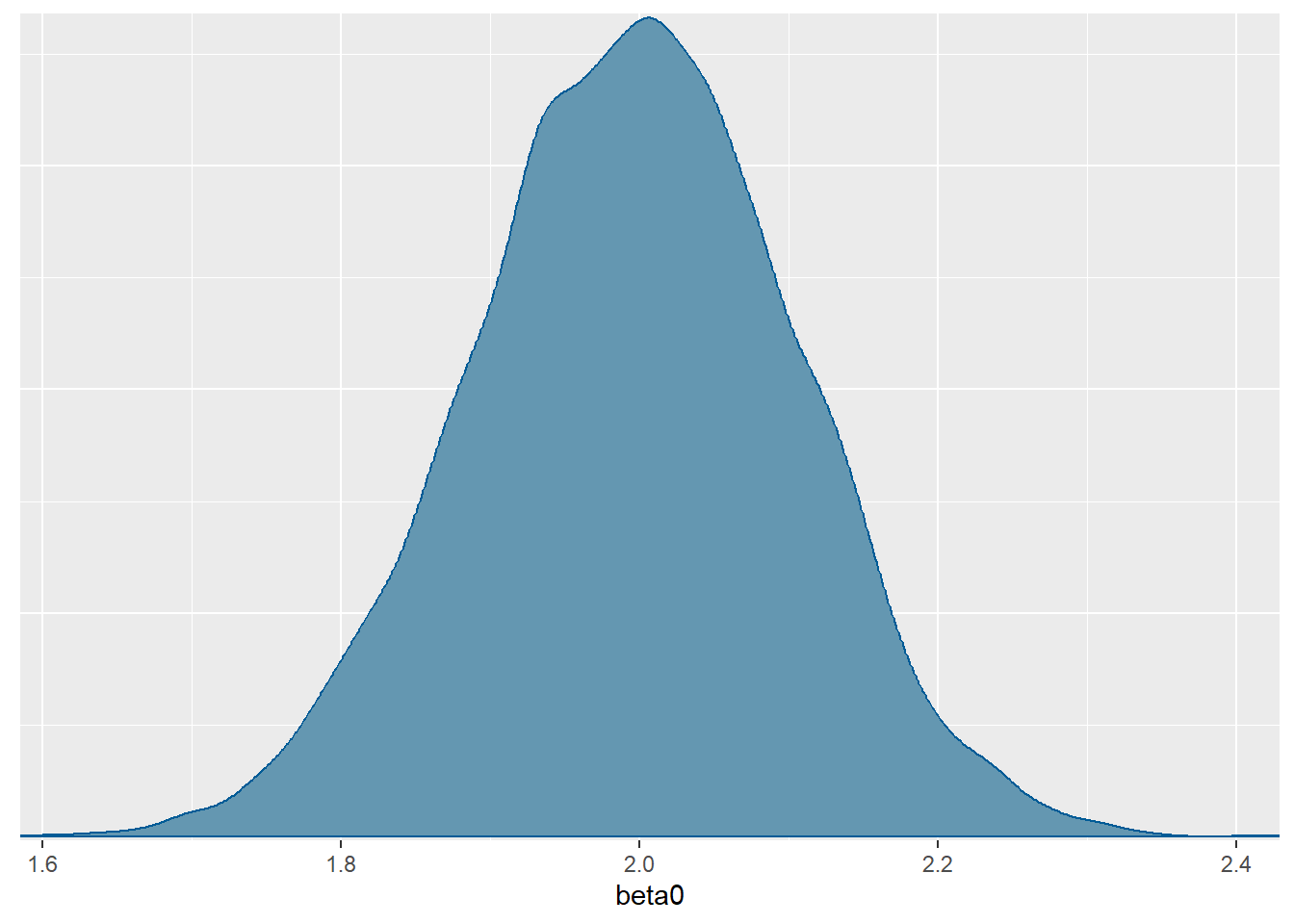
mcmc_dens(model.airbnb.sim, pars="y_tilda")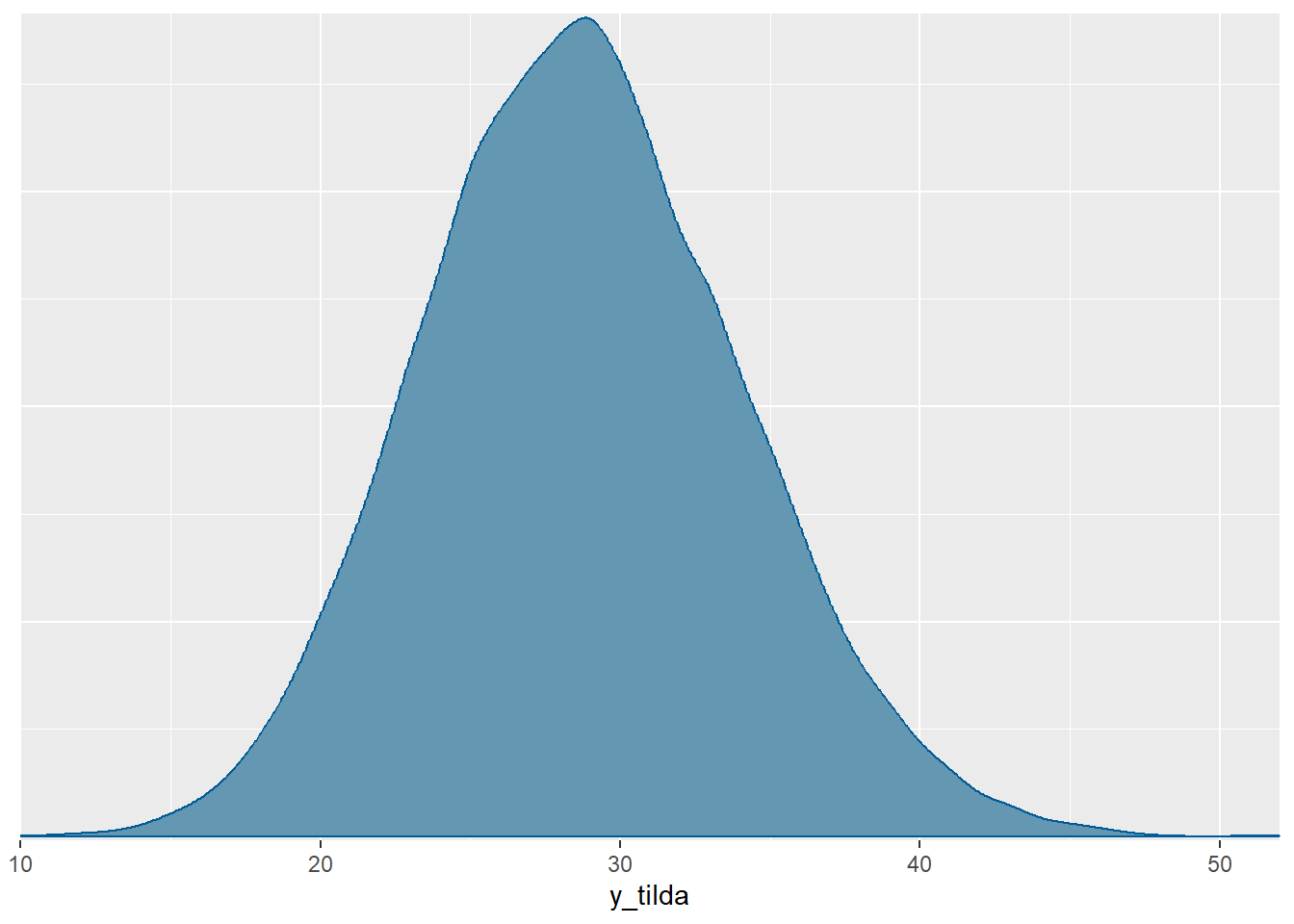
MCMC.airbnb <- rstan:: extract(model.airbnb.sim)
1-ecdf(MCMC.airbnb$y_tilda)(30)[1] 0.35515- Odgovor nam daje parametar \(\beta_1\), odnosno pripadna posteriorna distribucija. Prema modelu, očekujemo povećanje između \(12 \%\) i \(17 \%\) povećanja broja recenzija s \(95\%\) vjerojatnosti. Uzmemo li u obzir posteriorno očekivanje parametra \(\beta_1\), možemo reći da prema modelu očekujemo približno povećanje u iznosu \(14 \%\) broja novih recenzija za svako polovično povećanje ocjena smještaja.
mcmc_dens(model.airbnb.sim, pars="beta1")