6 Bayesovski hijerarhijski modeli

Izmjenljivost (eng. Exchangeability)

Neka je \(f(x_1, \dots, x_n)\) zajednička gustoća slučajnog vektora \((X_1, \dots, X_n)\). Ako je \(f(x_1, \dots, x_n)=f(x_{\pi_1}, \dots, x_{\pi_n})\) za sve permutacije \(\pi\) skupa \(\{1, \dots, n\}\), tada kažemo da su slučajne varijable \(X_1, \dots X_n\) izmjenljive.

Sljedeća dva teorema povezuju Bayesovski koncept i koncept izmjenljivosti.

j.s.u. i izmjenljivost

Teorem 6.1 Neka je \(\theta ~ f(\theta)\) i \(X_1, \dots, X_n\) uvjetno nezavisne i jednako distribuirane uz dani \(\theta\). Tada su \(X_1, \dots, X_n\) izmjenljive.

Drugim riječima:

\[\begin{array}{rr} X_1, \dots, X_n | \theta\,\, n.j.d. \\ \theta \sim f(\theta) \quad \end{array} \Rightarrow \quad X_1, \dots, X_n \text{ su izmjenljive }.\]

O suprotnom smjeru govori sljedeći teorem.

de Finetti

Teorem 6.2 Neka \((X_n, \, n \in \mathbb{N})\) niz slučajnih varijabli takvih da je \(\mathcal{R}(X_i)=\mathcal{R}(X_j), \forall i, j \in \mathbb{N}\). Neka su \(X_1, \dots, X_n\) izmjelnjive za svaki \(n \in \mathbb{N}\). Tada je \[f(x_1, \dots, x_n)=\int \prod_{i=1}^{n}f(x_i | \theta)f(\theta)d \theta\] za neki parametar \(\theta\) uz apriornu distribuciju \(f(\theta)\) i neku vjerodostojnosti \(f(x | \theta)\). Pri tome apriorna distribucija i vjerodostojnost ovise o \(f(x_1, \dots, x_n)\).

Zaključujemo:

\[\begin{array}{rr} X_1, \dots, X_n | \theta\,\, n.j.d. \text{ za svaki n } \in \mathbb{N} \\ \theta \sim f(\theta) \quad \end{array} \Leftrightarrow \quad X_1, \dots, X_n \text{ su izmjenljive za svaki } n \in \mathbb{N}.\]

Realni scenariji za “\(X_1, \dots, X_n\) izmjenljive za svaki \(n\in \mathbb{N}\)”:

\(X_1, \dots, X_n\) su dobiveni uzorkovanjem iz konačne populacije s vraćanjem
\(X_1, \dots, X_n\) su dobiveni uzorkovanjem iz beskonačne populacije s vraćanjem (u praksi, ako je populacije dimenzije \(N\) bit će dovoljno \(N>>n\))
\(X_1, \dots, X_n\) su ishodi ponovljivog pokusa.

Terminologija za hijerarhijske modele nije konzistentna te se isti mogu pronaći pod nazivom “fixed effects” ili “random effects” modeli.

Pretpostavimo da imamo hijerarhijske podatke \((\mathbb{X}_1, \dots, \mathbb{X}_m)\), gdje je \(\mathbb{X}_j=(X_{1,j}, \dots X_{n_j, j})\) (usporedba \(m\) grupa svaka dimenzije uzorka \(n_j, \, j \in \{1, \dots, m\}\)).

Pri tome:

Ako je jedino što znamo da je \((X_{1, j}, \dots, X_{n_j, j})\) slučajan uzorak iz grupe \(j\), tretiramo ih kao izmjenljive.
Ako je \(N_j >> n_j\): \(\{X_{1, j}, \dots, X_{n_j, j} | \phi_j\}\) j.s.u. iz \(f(x | \phi_j), \, j=1, \dots, m\) (prema de Finettijevom teoremu).
Ako su grupe uzorkovane iz veće populacije grupa i za njih možemo primijeniti izmjenljiv model: \(\{\phi_1, \dots, \phi_m | \psi \}\) j.s.u. iz \(f(\phi | \psi)\) (ponovo prema de Finettijevom teoremu).

Ovom uzastopnom primjenom de Finettijevog teorema dobivamo:

Bayesovski hijerarhijski model

\[\begin{align*} X_{1, j}, \dots, X_{n_j, j} | \phi_j &\, \text{ j.s.u. iz } f(x | \phi_j) ( \text{varijabilnost uzorkovanja unutar grupe} ) \\ \phi_{1}, \dots, \phi_{m} | \psi &\, \text{ j.s.u. iz } f(\phi | \psi) ( \text{varijabilnost uzorkovanja među grupama} ) \\ \psi \sim & f(\psi) ( \text{ apriorna distrribucija} ) \end{align*}\]

Primijetimo da iz podataka procjenjujemo uzoračke distribucije \(f(x | \phi)\) i \(f(\phi | \psi)\), dk se apriorna distribucija ne procjenjuje iz podataka.

6.1 Hijerarhijski normalni model (homogene varijance)

Radi se o popularnom modelu za opisivanje heterogenosti očekivanja više populacija.

Bayesovski normalni hijerarhijski model

\[\begin{align*} X_{1, j}, \dots, X_{n_j, j} | \theta_j, \, \sigma^2 &\, \text{ j.s.u. iz } \mathcal{N}(\theta_j, \sigma^2), j \in \{1, \dots, m\} ( \text{varijabilnost uzorkovanja unutar grupe} ) \\ \theta_{1}, \dots, \theta_{m} | \mu, \tau^2 &\, \text{ j.s.u. iz } \mathcal{N}(\mu, \tau^2) ( \text{varijabilnost uzorkovanja među grupama} ) \end{align*}\]

Možemo identificirati \(\phi_j=\left(\theta_j, \sigma^2\right)\) i \(\psi =(\mu, \tau^2)\). Pri tome su (fiksni) nepoznati parametri \(\sigma^2>0, \, \mu \in \mathbb{R}, \, \tau^2 >0\). Za njih prepostaje postaviti apriorne distribucije kako bi kompletirali Bayesovski hijerarhijski model.

Ukoliko želimo kreirati aproksimaciju posteriorne distribucije parametara koristeći Gibbsovo uzorkovanje, postavit ćemo sljedeće (semi)konjugatne apriorne distribucije:

\[\begin{align*} 1/\sigma^2 &\sim \Gamma(\nu_0 /2, \nu_0 \sigma^2_0/2) \\ 1/\tau^2 & \sim \Gamma(\eta_0/2, \eta_0 \tau^2_0/2) \\ \mu & \mathcal{N}(\mu_0, \gamma^2_0). \end{align*}\]

U konačnici nas zanima MCMC aproskimacija posteriorne distribucije \[f(\theta_1, \dots, \theta_m, \mu, \tau^2, \sigma^2 | \mathbb{x}_1, \dots, \mathbb{x}_m) \propto f(\mu) f(\tau^2) f(\sigma^2) \left[\prod_{j=1}^{m} f(\theta_j | \mu, \tau^2)\right] \cdot \left[\prod_{j=1}^{m} \prod_{i=1}^{n_j}f(x_{i,j} | \theta_j, \sigma^2)\right].\]

Uvjetne posteriorne distribucije za \(\mu\) i \(\tau^2\):

\[\begin{align*} \{\mu &| \theta_1, \dots, \theta_m, \tau^2 \} \sim \mathcal{N}\left(\frac{m \bar{\theta}/\tau^2+\mu_0 /\gamma^2_0}{m/\tau^2+1 /\gamma^2_0}, \, \frac{1}{m /\tau^2 + 1/ \gamma^2_0}\right) \\ \{\frac{1}{\tau^2} &| \theta_1, \dots, \theta_m, \mu\} \sim \Gamma\left(\frac{\eta_0 +m}{2}, \frac{\eta_0 \tau^2_0 + \sum_j (\theta_j-\mu)^2}{2} \right) \end{align*}\]

Uvjetne distribucije za \(\theta_j\):

\[\{\theta_j | x_{1,j}, \dots, x_{n_j, j}, \sigma^2\} \sim \mathcal{N}\left(\frac{n_j \bar{x}_j/\sigma^2+\mu / \tau^2}{n_j/\sigma^2+1/\sigma^2}, \frac{1}{n_j/\sigma^2+1/\tau^2}\right)\] - Uvjetna distribucija od \(\sigma^2\) (koncetrirana oko zajedničke uzoračke procjene varijance):

\[\{1/\sigma^2 | \theta_1, \dots, \theta_m, \mathbb{x}_1, \dots, \mathbb{x}_m\} \sim \Gamma \left(\frac{1}{2}(\nu_0+\sum_{j=1}^{m}n_j), \frac{1}{2}\left(\nu_0 \sigma^2_0 + \sum_{j=1}^{m}\sum_{i=1}^{n_j}(x_{i, j} - \theta_j)^2\right)\right)\]

Konačno, Gibbsovo uzorkovanje za \(\phi^{(s)}=\left(\theta^{(s)}_1, \dots, \theta^{(s)}_m, \mu^{(s)}, \tau^{2(s)}, \sigma^{2(s)}\right)\):

Generiraj \(\mu^{(s+1)} \sim f(\mu | \theta^{(s)}_1, \dots, \theta^{(s)}_m, \tau^{2(s)})\)
Generiraj \(\tau^{2(s+1)} \sim f(\tau^{2} | \theta^{(s)}_1, \dots, \theta^{(s)}_m, \mu^{s+1})\)
Generiraj \(\sigma^{2(s+1)} \sim f(\sigma^2 | \theta^{(s)}_1, \dots, \theta^{(s)}_m, \mathbb{x}_1, \dots, \mathbb{x}_m)\)
\(\forall j \in \{1, \dots, m\}\) generiraj \(\theta^{(s+1)}_j \sim f(\theta_j | \mu^{(s+1)}, \tau^{2(s+1)}, \sigma^{2(s+1)}, \mathbb{x}_j)\)

6.2 Hijerarhijski normalni model (različite varijance)

Dodatno se pretpostavlja da osim populacijskih očekivanja, postoje razlike i u varijabilnosti (\(\sigma^2_j\) je varijabinost za grupu \(j\)).

Bayesovski normalni hijerarhijski model (različite varijance)

\[\begin{align*} X_{1, j}, \dots, X_{n_j, j} | \theta_j, \, \sigma^2_j &\, \text{ j.s.u. iz } \mathcal{N}(\theta_j, \sigma^2_j), j \in \{1, \dots, m\} ( \text{varijabilnost uzorkovanja unutar grupe} ) \\ \theta_{1}, \dots, \theta_{m} | \mu, \tau^2 &\, \text{ j.s.u. iz } \mathcal{N}(\mu, \tau^2) ( \text{varijabilnost uzorkovanja među grupama} ) \\ \sigma^2_{1}, \dots, \sigma^2_{m} | \nu_0, \sigma^2_0 &\, \text{ j.s.u. iz } \Gamma(\nu_0/2, \nu_0 \sigma^2_0 /2) ( \text{varijabilnost uzorkovanja među grupama} ) \end{align*}\]

Slično kao i u prošlom modelu slijedi

\[\{\theta_j | X_{1,j} \dots, X_{n_j, j}, \sigma^2_j\} \sim \mathcal{N}\left(\frac{n_j \bar{x}_j/\sigma^2_j+\mu / \tau^2}{n_j/\sigma^2_j+1/\sigma^2_j}, \frac{1}{n_j/\sigma^2_j+1/\tau^2}\right)\] Uz apriornu distribuciju \(\sigma^2_0 \sim \Gamma(a,b)\) slijedi \[\{\sigma^2_0 | \sigma^2_1, \dots, \sigma^2_m, \mu_0\} \sim \Gamma \left(a+\frac{1}{2}m \nu_0, b+ \frac{1}{2}\sum_{j=1}^{m}(1/\sigma^2_j)^2\right).\] Za \(\nu_0\) nema jednostavnog konjugata.

Primjer - hijerarhijski normalni model (poznata varijanca)

Podaci (http://www2.stat.duke.edu/~pdh10/FCBS/Replication/nels.RData)

Provedena je studija o rezultatima u matematici učenika istih uzrasta različitih škola u SAD-u. Želimo ustvrditi postoje li razlike u očekivanim rezultatima po školama.

Kod - Gibbsovo uzorkovanje

## vrijednosti hiperparametara apriorne distribucije

load(file="C:/Users/Korisnik/Desktop/OneDrive - Sveučilište Josipa Jurja Strossmayera Osijek/Fakultet_nastava/nastava/Aktualne_teme_iz_statistike/Bayesovska_statistika/Bayesovska_statistika_Quarto/baze/nels.RData")


#### tehnicki detalji - reorganizacija podataka u listu
Y<-list()
YM<-NULL
J<-max(Y.school.mathscore[,1])
n<-ybar<-ymed<-s2<-rep(0,J)
for(j in 1:J) {
  Y[[j]]<-Y.school.mathscore[ Y.school.mathscore[,1]==j,2] 
  ybar[j]<-mean(Y[[j]])
  ymed[j]<-median(Y[[j]])
  n[j]<-length(Y[[j]])
  s2[j]<-var(Y[[j]])
  YM<-rbind( YM, cbind( rep(j,n[j]), Y[[j]] ))
               }

colnames(YM)<-c("school","mathscore")

nu0<-1  ; s20<-100
eta0<-1 ; t20<-100
mu0<-50 ; g20<-25

## početne vrijednosti
m<-length(Y) 
n<-sv<-ybar<-rep(NA,m) 
for(j in 1:m) 
{ 
  ybar[j]<-mean(Y[[j]])
  sv[j]<-var(Y[[j]])
  n[j]<-length(Y[[j]]) 
}
theta<-ybar
sigma2<-mean(sv)
mu<-mean(theta)
tau2<-var(theta)

## postavke za MCMC
set.seed(1)
S<-5000
THETA<-matrix( nrow=S,ncol=m)
MST<-matrix( nrow=S,ncol=3)

## MCMC algoritam
for(s in 1:S) 
{

  # generiranje novih theta iz uvjetne distribucije uz ostale vrijednosti poznate
  for(j in 1:m) 
  {
    vtheta<-1/(n[j]/sigma2+1/tau2)
    etheta<-vtheta*(ybar[j]*n[j]/sigma2+mu/tau2)
    theta[j]<-rnorm(1,etheta,sqrt(vtheta))
   }

  #generiranje novog sigma^2 iz uvjetne distribucije uz ostale vrijednosti poznate
  nun<-nu0+sum(n)
  ss<-nu0*s20;for(j in 1:m){ss<-ss+sum((Y[[j]]-theta[j])^2)}
  sigma2<-1/rgamma(1,nun/2,ss/2)

  #generiranje novog mu iz uvjetne distribucije uz ostale vrijednosti poznate
  vmu<- 1/(m/tau2+1/g20)
  emu<- vmu*(m*mean(theta)/tau2 + mu0/g20)
  mu<-rnorm(1,emu,sqrt(vmu)) 

  # generiranje novog tau iz uvjetne distribucije uz ostale vrijednosti poznate
  etam<-eta0+m
  ss<- eta0*t20 + sum( (theta-mu)^2 )
  tau2<-1/rgamma(1,etam/2,ss/2)

  #spremanje simulacije
  THETA[s,]<-theta
  MST[s,]<-c(mu,sigma2,tau2)
}
mcmc1<-list(THETA=THETA,MST=MST)
stationarity.plot<-function(x,...)
{
S<-length(x)
scan<-1:S
ng<-min( round(S/100),10)
group<-S*ceiling( ng*scan/S) /ng
boxplot(x~group,...)            
}

Sljedeći kod grafički ilustrira je li došlo do konvergencije pomoću kutijastog dijagrama za svakih 500 uzastopnih simuliranih vrijednosti parametra iz MCMC metode. U slučaju da nije došlo do konvergencije, uočili bi značajnije razlike u raspodjeli simuliranih vrijednosti kako broj iteracija raste. Graf sugerira da je došlo do konvergencije.

Kod - Grafička ilustracija konvergencije MCMC metode pomoću boxplota

par(mfrow=c(1,3))
stationarity.plot(MST[,1],xlab="iteracija",ylab=expression(mu))
stationarity.plot(MST[,2],xlab="iteracija",ylab=expression(sigma^2))
stationarity.plot(MST[,3],xlab="iteracija",ylab=expression(tau^2))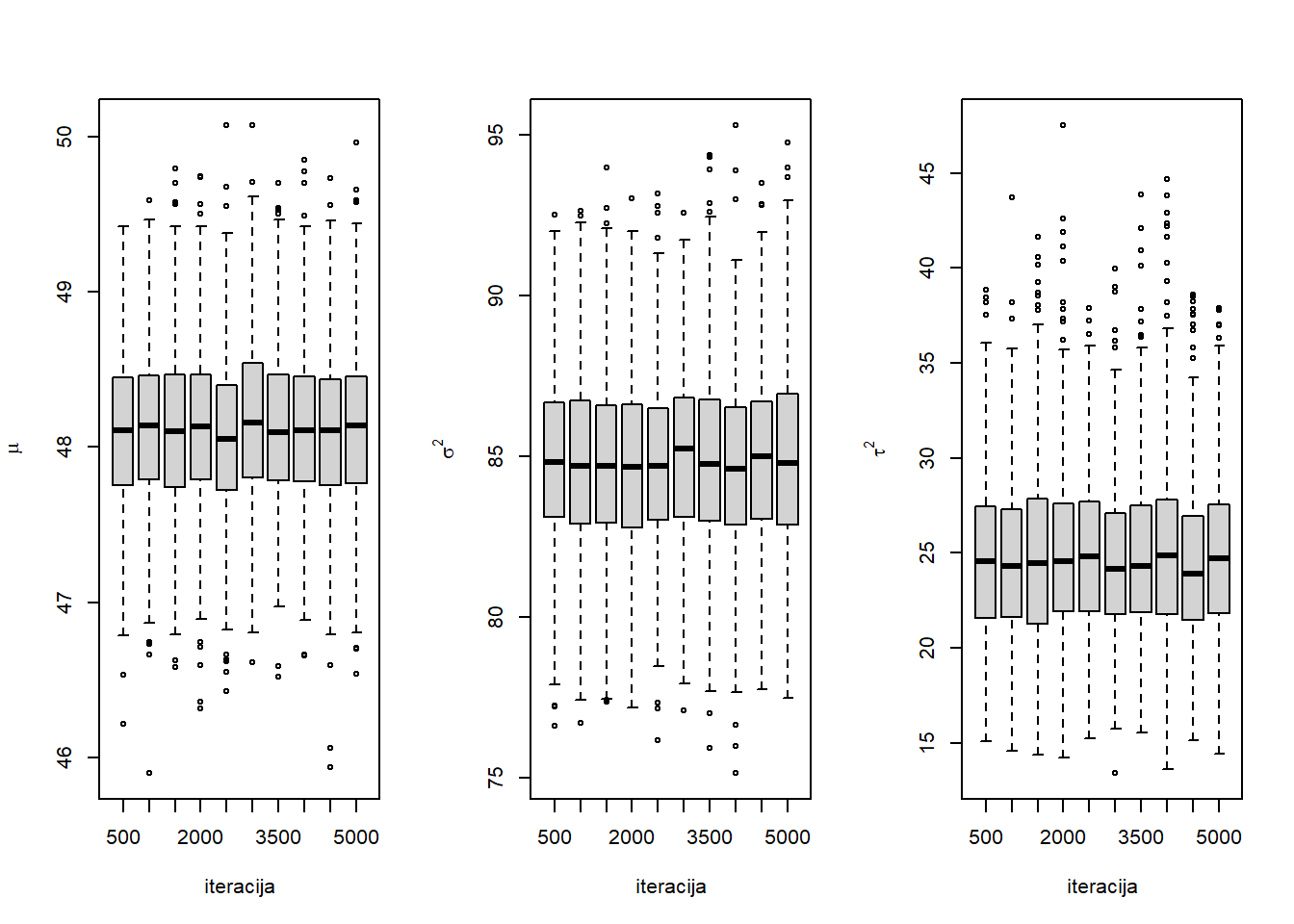

Kod - MCMC aproksimacije posteriorne gustoće parametara

par(mfrow=c(1,3),mar=c(2.75,2.75,.5,.5),mgp=c(1.7,.7,0))
plot(density(MST[,1],adj=2),xlab=expression(mu),main="",lwd=2,
ylab=expression(paste(italic("p("),mu,"|",italic(y[1]),"...",italic(y[m]),")")))
abline( v=quantile(MST[,1],c(.025,.5,.975)),col="gray",lty=c(3,2,3) )
plot(density(MST[,2],adj=2),xlab=expression(sigma^2),main="", lwd=2,
ylab=expression(paste(italic("p("),sigma^2,"|",italic(y[1]),"...",italic(y[m]),")")))
abline( v=quantile(MST[,2],c(.025,.5,.975)),col="gray",lty=c(3,2,3) )
plot(density(MST[,3],adj=2),xlab=expression(tau^2),main="",lwd=2,
ylab=expression(paste(italic("p("),tau^2,"|",italic(y[1]),"...",italic(y[m]),")")))
abline( v=quantile(MST[,3],c(.025,.5,.975)),col="gray",lty=c(3,2,3) )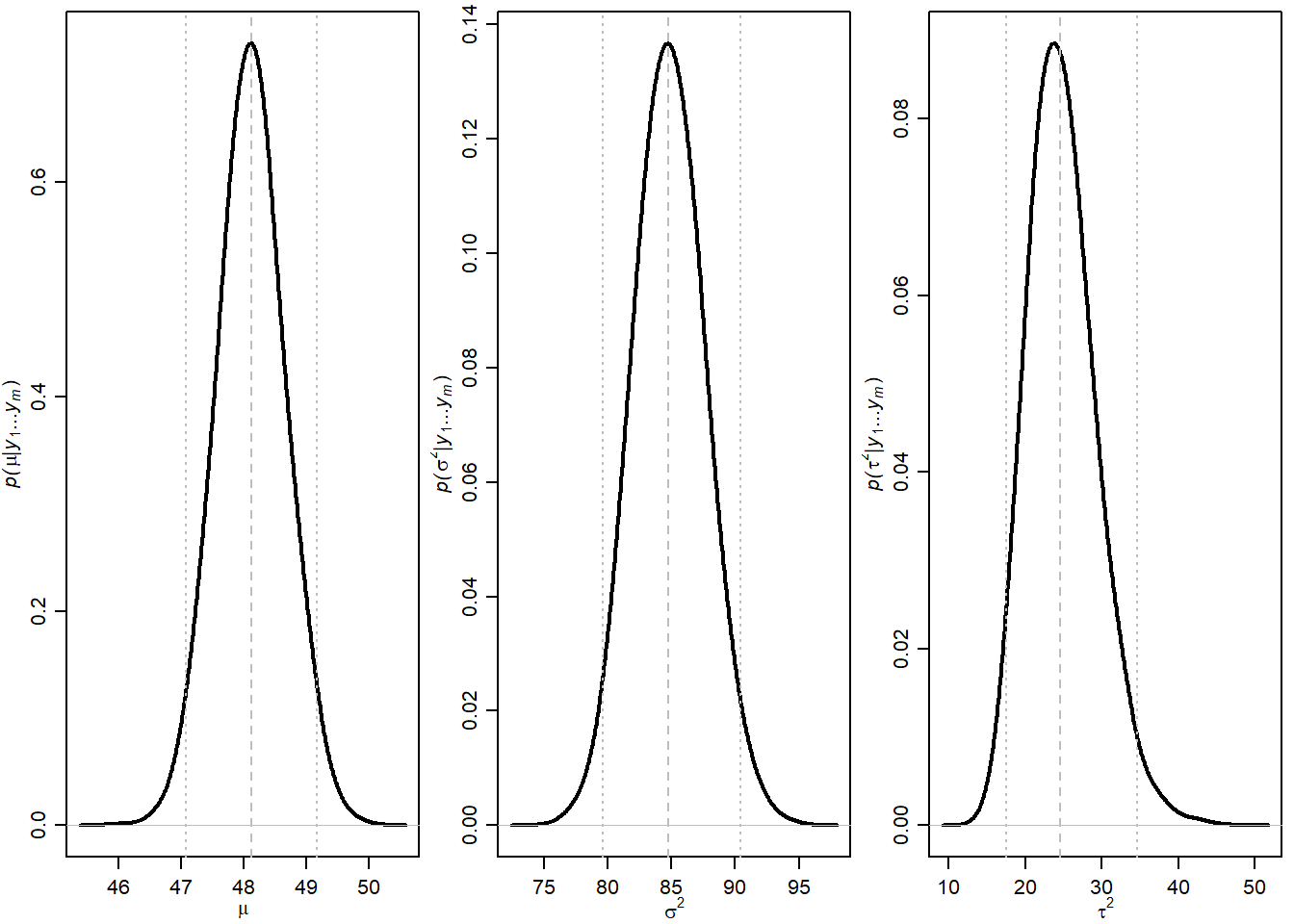

Hijerarhijski model implicira da su očekivane vrijednosti \(\theta_j\) (uvjetno na podatke, \(\mu, \tau^2, \sigma^2\)) težinska sredina \(\bar{x}_j\) i \(\mu\): \[E\left[\theta_j | \mathbb{x}_j, \mu , \tau, \sigma \right]= \frac{\bar{x}_j n_j /\sigma^2 + \mu/\tau^2}{n_j/\sigma^2+1/\tau^2}\] To implicira da je očekivana vrijednost \(\theta_j\) pomaknuta od prosjeka \(\bar{x}_j\) prema \(\mu\) za iznos koji ovisi o broju podataka u grupi \(j\) - \(n_j\). Taj efekt se naziva efekt skupljanja (eng. “shrinkage”) što ilustrira sljedeći grafički prikaz. Uočavamo da velike vrijednosti prosjeka odgovaraju nešto većim vrijednostima \(\hat{\theta}=E\left[\theta_j | \mathbb{x}_1, \dots, \mathbb{x}_m\right]\), i obratno. Drugi dio grafičkog prikaza sugerira da je efekt veći što je broj podataka u grupi manji. Drugim riječima, ako imamo puno podataka, nećemo imati potrebu koristiti informacije iz drugih grupa, tj. one neće imati efekta.

Kod - grafička ilustracija efekta skupljanja (eng. shrinkage)

par(mar=c(3,3,1,1),mgp=c(1.75,.75,0))
par(mfrow=c(1,2))

theta.hat<-apply(THETA,2,mean)
plot(ybar,theta.hat,xlab=expression(bar(italic(y))),ylab=expression(hat(theta)))
abline(0,1)
plot(n,ybar-theta.hat,ylab=expression( bar(italic(y))-hat(theta) ),xlab="sample size")
abline(h=0)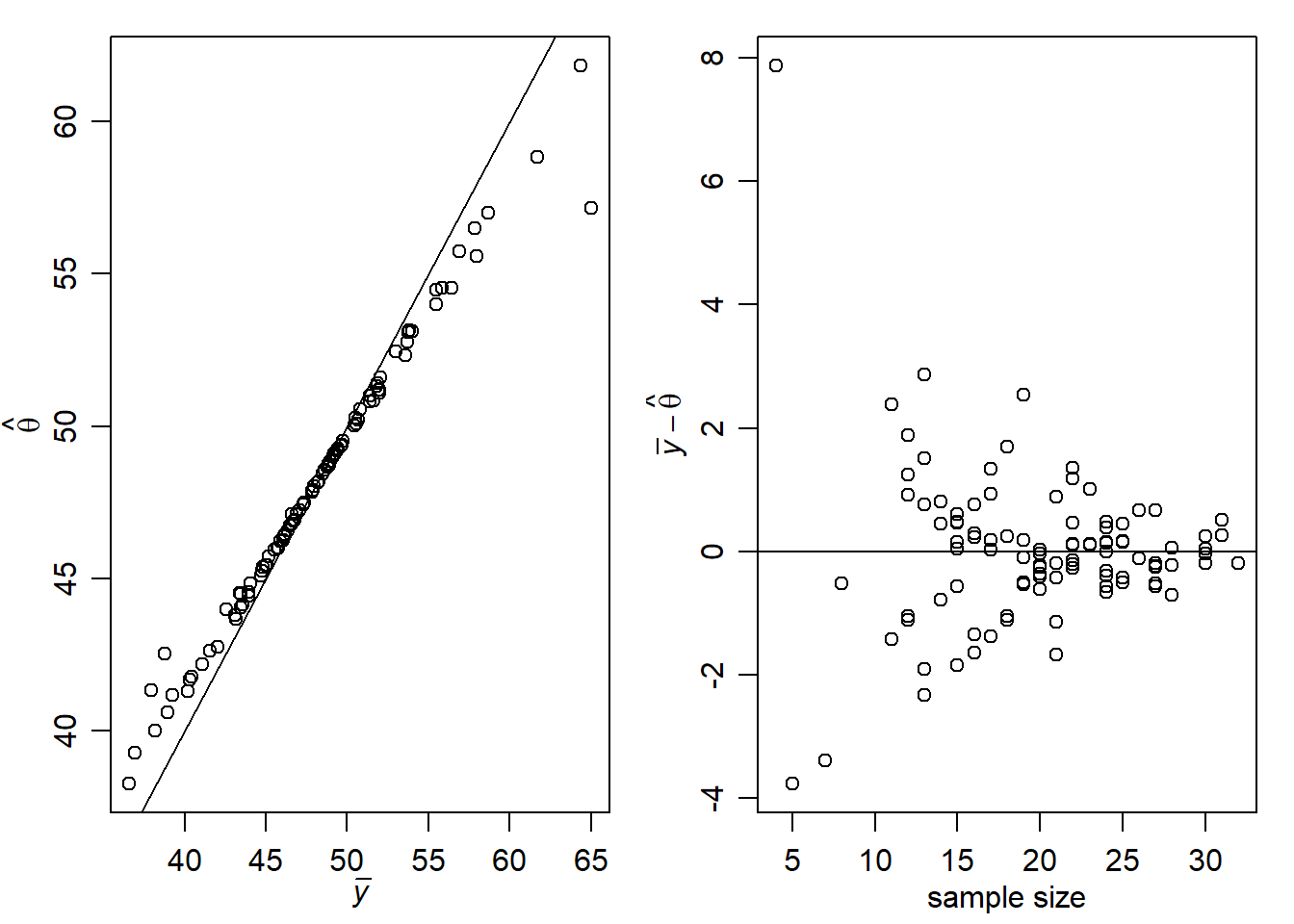

Ukoliko bismo htjeli rangirati rezultate škola prema očekivanim vrijednostima Bayesov pristup bi koristio posteriorna očekivanja \[E\left[\theta_1 | \mathbb{x}_1, \dots, \mathbb{x}_m\right], \cdots, E\left[\theta_m | \mathbb{x}_1, \dots, \mathbb{x}_m\right]\] dok bi ignorirajući hijerarhijski model koristili prosjeke pojedinih grupa kao procjene očekivanja \[\bar{x}_1, \dots, \bar{x}_m.\] Potonju metodu možemo doživjeti kao usporedbu očekivanja nezavisnih populacija (ANOVA).

Iako metode daju slične rezultate, ne u potpunosti iste. Primjerice za škole \(46\) i \(82\) bismo dobili drugačije rezultate, što ilustrira sljedeći grafički prikaz (male točke prikazuju podatke, dok velike točke prosjeke pripadnih škola). Ideja je da za školu \(46\) imamo više podataka te smo uvjereniji u rezultat prosjeka te se posljedično manje skuplja prema zajedničkom populacijskom očekivanju \(E[\mu | \mathbb{x}_1, \dots, \mathbb{x}_n]\). S druge strane za školu \(82\) imamo malo podataka te smo manje uvjereni u dobiveni prosjek (moguće je da se radi o djeci s lošijim rezultatima).

Kod - različito rangiranje dviju škola (Hijerarhijski model vs standardni)

par(mar=c(3,3,1,1),mgp=c(1.75,.75,0))

theta.order<-order(theta.hat)

idx<-c(46,82)

ybar.order<-order(ybar)

par(mfrow=c(1,1))
plot(density(THETA[,46],adj=2),col="black",xlim=
  range(c(Y[[46]],Y[[82]],THETA[,c(46,82)])),lwd=2,
        main="",xlab="math score",ylim=c(-.05,.2),ylab="",yaxt="n")
axis(side=2,at=c(0,0.10,0.20) )
lines(density(THETA[,82],adj=2),col="gray",lwd=2)
abline(h=0)

points( Y[[46]],rep(-0.01666,n[46]), col="black",pch=16)
points( ybar[46],-.01666,col="black",pch=16 ,cex=1.5)
abline( h=-.01666,col="black")

points( Y[[82]],rep(-0.0333,n[82]), col="gray",pch=16)
points( ybar[82],-.0333,col="gray",pch=16 ,cex=1.5)
abline( h=-.0333,col="gray")

segments(mean(MST[,1]), 0,mean(MST[,1]),1,lwd=2,lty=2 )

legend(52.5,.15,legend=c("school 46","school 82",
     expression(paste("E[", mu,"|",italic(y[1]),"...",italic(y[m]),"]"))),
       lwd=c(2,2),lty=c(1,1,2),col=c("black","gray"),bty="n")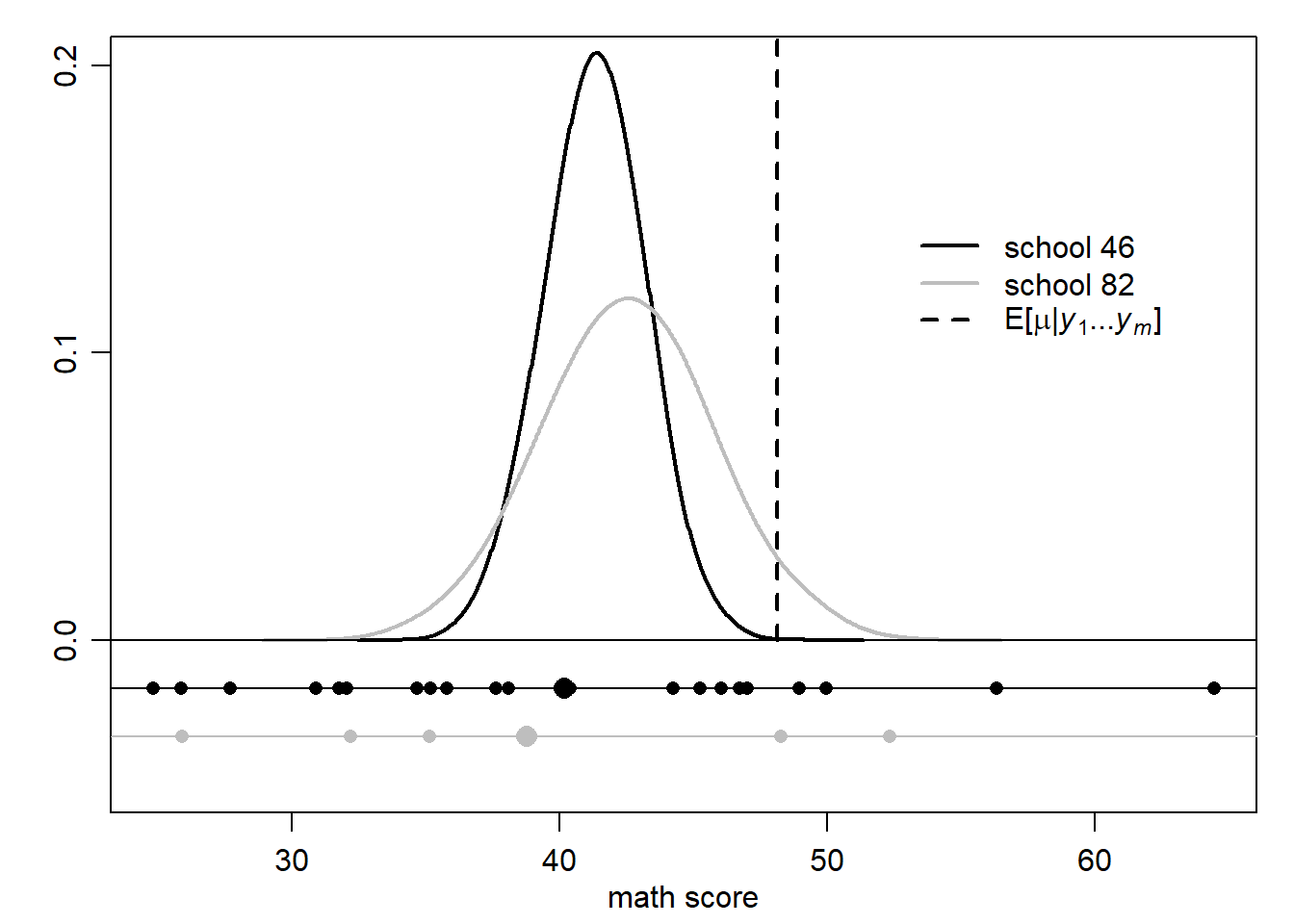

Zadatak 6.1 U osam različitih škola proveden je jednokratni program instrukcija u svrhu poboljšanja rezultata studenata na standardiziranim (SAT) testovima. Rezultati su prikazani u sljedećoj tablici. Pretpostavka je da podaci dolaze iz normalne distribucije. Koristite platformu STAN.

Škola	Izmjereni efekt	Standardna greška
1	28	15
2	8	10
3	-3	16
4	7	11
5	-1	9
6	1	11
7	18	10
8	12	18

Implementirajte Bayesov model koji tretira svaku školu zasebno (no pooling).
Implementirajte Bayesov model koji tretira sve škole zajedno (complete pooling).
Implementirajte hijerarhijski Bayesov model za isti problem.
Usporedite posteriorna očekivanja parametara za sva 3 modela.

Rješenje

model.a <-'data {
int<lower=0> J; //  broj škola
real y[J]; // izmjereni efekt za školu
real<lower=0> sigma[J]; // standardna greška izmjerenog efekta
}
parameters {
real theta[J]; // očekivani efekt škole
}
model {
y ~ normal(theta, sigma); //pretpostavljeni normalni model
}'

model.b <-'data {
int<lower=0> J; // broj škola
real y[J]; // izmjereni efekt za školu
real<lower=0> sigma[J]; // standardna greška izmjerenog efekta
}
parameters {
real theta; // zajednički očekivani efekt škola
}
model {
y ~ normal(theta, sigma); //pretpostavljeni normalni model
}'

model.c <-'data {
int<lower=0> J; //  broj škola
real y[J]; // izmjereni efekt za školu
real<lower=0> sigma[J]; // standardna greška izmjerenog efekta
}
parameters {
real theta[J]; // očekivani efekt škole
real mu; // zajedničko očekivanje škola
real<lower=0> tau; // varijabilnost među školama
}
model {
theta ~ normal(mu, tau); 
y ~ normal(theta, sigma); //pretpostavljeni normalni model
}'

podaci<- list(J=8, y=c(28,8,-3,7,-1,1,18,12), sigma = c(15,10,16,11,9,11,10,18))

model.a.sim <-
  stan(model_code = model.a,
       data = list(J=8, y=c(28,8,-3,7,-1,1,18,12), sigma = c(15,10,16,11,9,11,10,18)),
       chains = 4, iter = 5000*2, cores=1, refresh=0, seed = 934)


model.b.sim <-
  stan(model_code = model.b,
       data = list(J=8, y=c(28,8,-3,7,-1,1,18,12), sigma = c(15,10,16,11,9,11,10,18)),
       chains = 4, iter = 5000*2, cores=1, refresh=0, seed = 934)

model.c.sim <-
  stan(model_code = model.c,
       data = list(J=8, y=c(28,8,-3,7,-1,1,18,12), sigma = c(15,10,16,11,9,11,10,18)),
       chains = 4, iter = 5000*2, cores=1, refresh=0, seed = 934)

Warning: There were 466 divergent transitions after warmup. See
https://mc-stan.org/misc/warnings.html#divergent-transitions-after-warmup
to find out why this is a problem and how to eliminate them.

Warning: Examine the pairs() plot to diagnose sampling problems

Warning: Tail Effective Samples Size (ESS) is too low, indicating posterior variances and tail quantiles may be unreliable.
Running the chains for more iterations may help. See
https://mc-stan.org/misc/warnings.html#tail-ess

print(model.a.sim)

Inference for Stan model: anon_model.
4 chains, each with iter=10000; warmup=5000; thin=1; 
post-warmup draws per chain=5000, total post-warmup draws=20000.

          mean se_mean    sd   2.5%    25%   50%   75% 97.5% n_eff Rhat
theta[1] 27.91    0.08 15.14  -1.69  17.56 28.01 38.21 57.12 35627    1
theta[2]  8.09    0.05 10.03 -11.59   1.27  8.05 14.91 27.80 34670    1
theta[3] -3.08    0.09 15.86 -33.73 -13.83 -3.18  7.65 28.07 33742    1
theta[4]  6.99    0.06 11.04 -14.83  -0.36  6.98 14.41 28.66 35686    1
theta[5] -0.99    0.05  9.08 -18.52  -7.20 -1.02  5.18 16.57 34417    1
theta[6]  1.02    0.06 10.97 -20.84  -6.26  1.03  8.35 22.61 35220    1
theta[7] 18.02    0.05 10.01  -1.59  11.22 18.00 24.84 37.68 35682    1
theta[8] 11.96    0.10 17.72 -22.76  -0.02 11.86 23.93 46.33 33297    1
lp__     -4.00    0.02  1.98  -8.66  -5.10 -3.68 -2.54 -1.11  9388    1

Samples were drawn using NUTS(diag_e) at Mon Jun  3 09:43:50 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

print(model.b.sim)

Inference for Stan model: anon_model.
4 chains, each with iter=10000; warmup=5000; thin=1; 
post-warmup draws per chain=5000, total post-warmup draws=20000.

       mean se_mean   sd  2.5%   25%   50%   75% 97.5% n_eff Rhat
theta  7.63    0.05 4.07 -0.27  4.83  7.61 10.43 15.52  7737    1
lp__  -2.85    0.01 0.68 -4.80 -3.03 -2.59 -2.41 -2.35  8799    1

Samples were drawn using NUTS(diag_e) at Mon Jun  3 09:44:38 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

print(model.c.sim)

Inference for Stan model: anon_model.
4 chains, each with iter=10000; warmup=5000; thin=1; 
post-warmup draws per chain=5000, total post-warmup draws=20000.

           mean se_mean   sd   2.5%    25%    50%    75% 97.5% n_eff Rhat
theta[1]  11.88    0.15 8.63  -2.11   6.18  10.74  16.34 32.23  3321 1.00
theta[2]   7.87    0.09 6.45  -4.95   3.79   7.80  11.88 21.23  5672 1.00
theta[3]   5.90    0.10 8.08 -12.44   1.49   6.37  10.85 20.98  6366 1.00
theta[4]   7.67    0.09 6.77  -6.02   3.56   7.61  11.80 21.45  5709 1.00
theta[5]   4.87    0.10 6.41  -9.10   1.03   5.26   9.18 16.38  4199 1.00
theta[6]   6.04    0.09 6.80  -8.55   1.90   6.35  10.42 18.96  5185 1.00
theta[7]  11.05    0.13 7.00  -1.03   6.35  10.47  15.14 26.65  3114 1.00
theta[8]   8.53    0.10 8.23  -7.45   3.65   8.27  13.10 26.09  6486 1.00
mu         8.02    0.10 5.22  -1.75   4.70   7.98  11.22 18.55  2938 1.00
tau        7.30    0.14 5.69   1.09   3.20   5.94   9.76 21.64  1614 1.00
lp__     -18.13    0.21 5.48 -27.97 -22.01 -18.63 -14.50 -6.51   700 1.01

Samples were drawn using NUTS(diag_e) at Mon Jun  3 09:45:25 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

Zadatak 6.2 U bazi podataka “Skole8.csv” nalaze se podaci o vremenu koje učenici provedu rješavajući zadaću na tjednoj bazi u osam različitih škola.

Predložite hijerarhijski normalni model (uz homogene varijance) za usporedbu očekivanih rezultata među školama. Pri tome koristite sljedeća apriorna uvjerenja:
- Zajedničko očekivanje svih škola ima normalnu distribuciju s očekivanjem 7 i varijancom 5.
- Varijabilnost (varijanca) među školama ima inverznu gama distribuciju s parametrima \(\eta_0=2\) i \(\tau^2_0\)=10
- Varijabilnost u podacima (varijanca) ima inverznu gama distribuciju s parametrima \(\nu_0=2\) i \(\sigma^2_0=15\).
Implementirajte model na platformi STAN i Odredite aproksimacije posteriornih distribucija za varijabilnost (varijancu) među podacima, zajedničko očekivanje škola i očekivanje treće škole.
Odredite aproksimaciju posteriornog očekivanog vremena učenika uloženog na rješavanje zadaće u ovisnosti o školi. Usporedite s prosječnim rezultatima po školama. Grafički usporedite. Postoje li razlike u rangiranju škola?
Odredite posteriornu vjerojatnost da učenici sedme škole očekivano manje provode vremena rješavajući zadaću na tjednoj bazi u odnosu na šesti školu.
Odredite posteriornu vjerojatnost da učenici sedme škole očekivano najmanje provode vremena rješavajući zadaću na tjednoj bazi.

Rješenje

skole <- 'data {
  int<lower=1> N; //ukupan broj podataka
  int<lower=1> j; // broj grupa
  vector[N] y; // podaci
  int n[j]; // velicina grupe
  real<lower=0> nu0; //hiperparametri
  real<lower=0> eta0;
  real<lower=0> tau20;
  real<lower=0> sigma20;
  real<lower=0> gama20;
  real<lower=0> mu0;
}
parameters {
  real<lower=0> tau2; // varijanca grupa
  real<lower=0> sigma2; // varijanca podataka
  real mu; // zajedničko očekivanje svih populacija
 real theta[j]; // očekivanje (efekt) grupa
  
}
model {
tau2 ~ inv_gamma(eta0/2, eta0*tau20/2);
sigma2 ~ inv_gamma(nu0/2, nu0*sigma20/2);
mu ~ normal(mu0, sqrt(gama20));
theta ~ normal(mu, sqrt(tau2));
int pos;
  pos = 1;
  for (k in 1:j) {
    segment(y, pos, n[k]) ~ normal(theta[k], sqrt(sigma2));
    pos = pos + n[k];
  }
}
'


baza.skole<-read.csv2("/Users/Korisnik/Desktop/OneDrive - Sveučilište Josipa Jurja Strossmayera Osijek/Fakultet_nastava/nastava/Aktualne_teme_iz_statistike/Bayesovska_statistika/Bayesovska_statistika_Quarto/baze/Skole8.csv")
attach(baza.skole)
skole8.podaci <- list(
  j = 8,
  N=length(Vrijeme),
  n=c(25, 23, 20, 24, 24, 22, 22, 20),
  y = Vrijeme,
  mu0=7,
  gama20=5,
  tau20=10,
  eta0=2,
  sigma20=15,
  nu0=2)

sim.MCMC.stan.skole <-stan(
  model_code = skole,
  data = skole8.podaci,    # named list of data
  chains = 4,             # broj korištenih Markovljevih lanaca
  warmup = 10000,          # burn in period za svaki lanac
  iter = 20000,            # ukupan broj iteracija svakog lanca
  cores = 1,              # broj korištenih jezgri
  refresh = 0,            # no progress show
  seed=934
)

Aproksimacija posteriorne distribucije za \(\sigma^2\):

mcmc_dens(sim.MCMC.stan.skole, pars = "sigma2") +   
  yaxis_text(TRUE) + 
  ylab("density")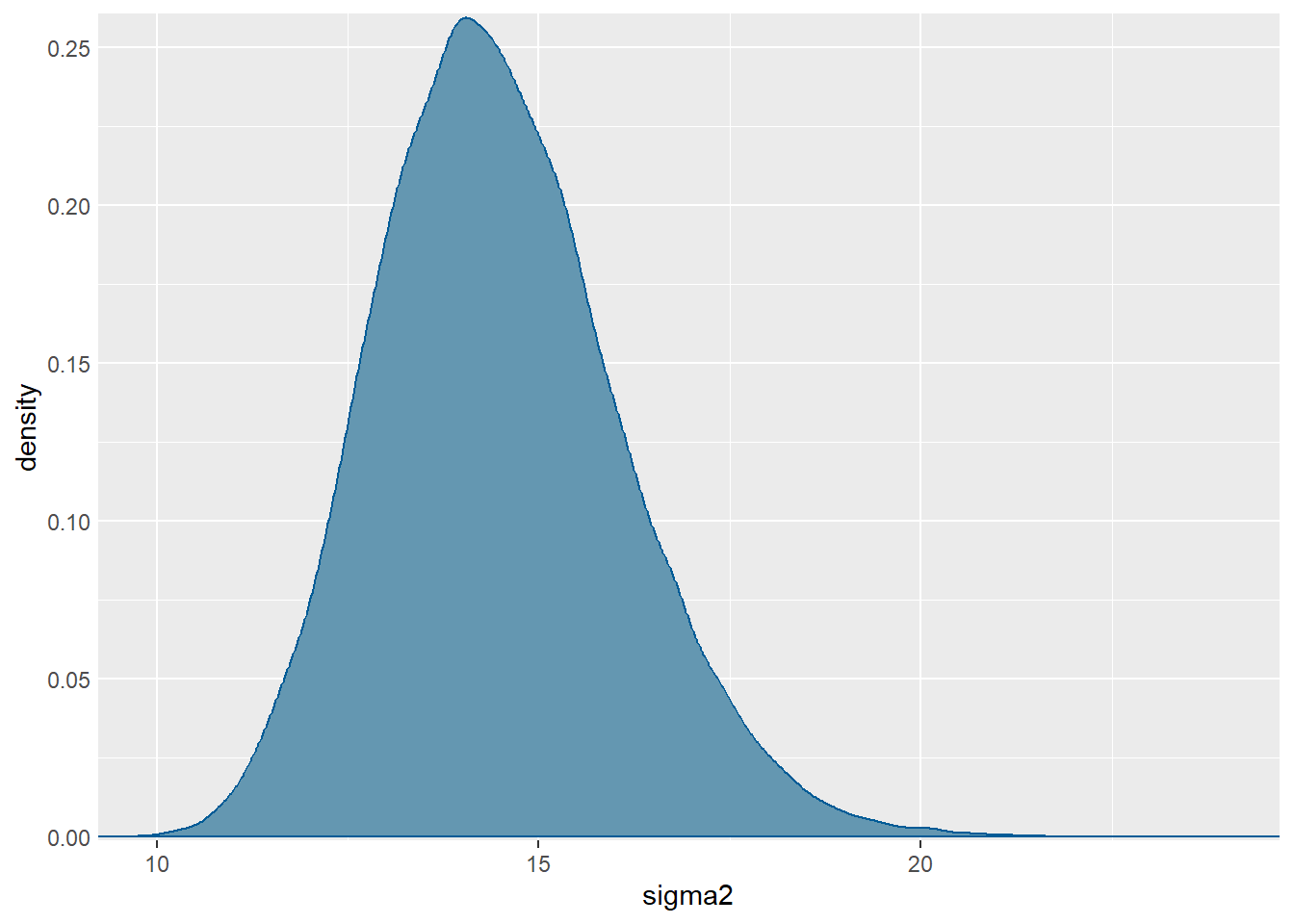

Aproksimacija posteriorne distribucije za \(\mu\):

mcmc_dens(sim.MCMC.stan.skole, pars = "mu") +   
  yaxis_text(TRUE) + 
  ylab("density")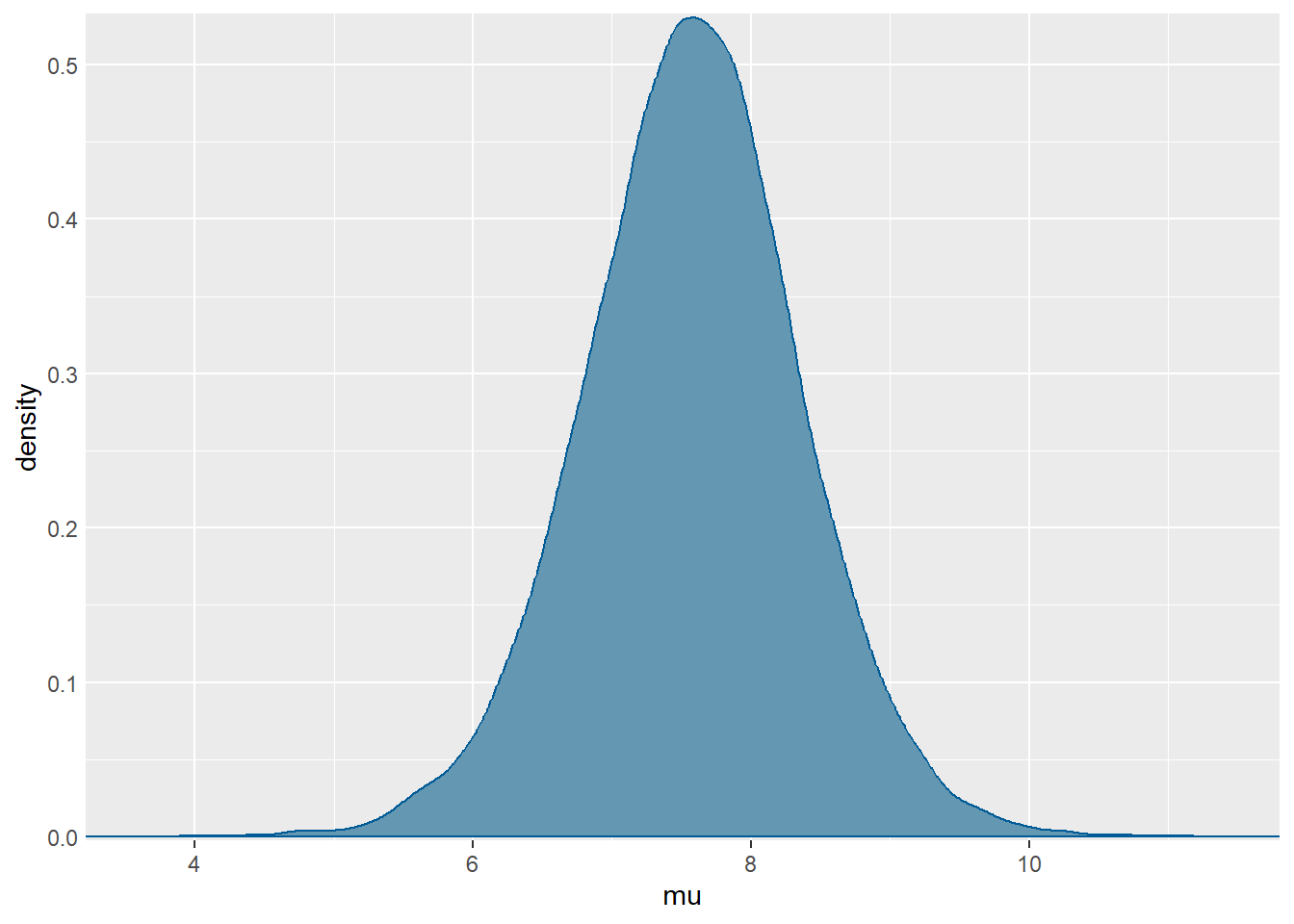

Aproksimacija posteriorne distribucije za \(\theta_3\):

mcmc_dens(sim.MCMC.stan.skole, pars = "theta[3]") +   
  yaxis_text(TRUE) + 
  ylab("density")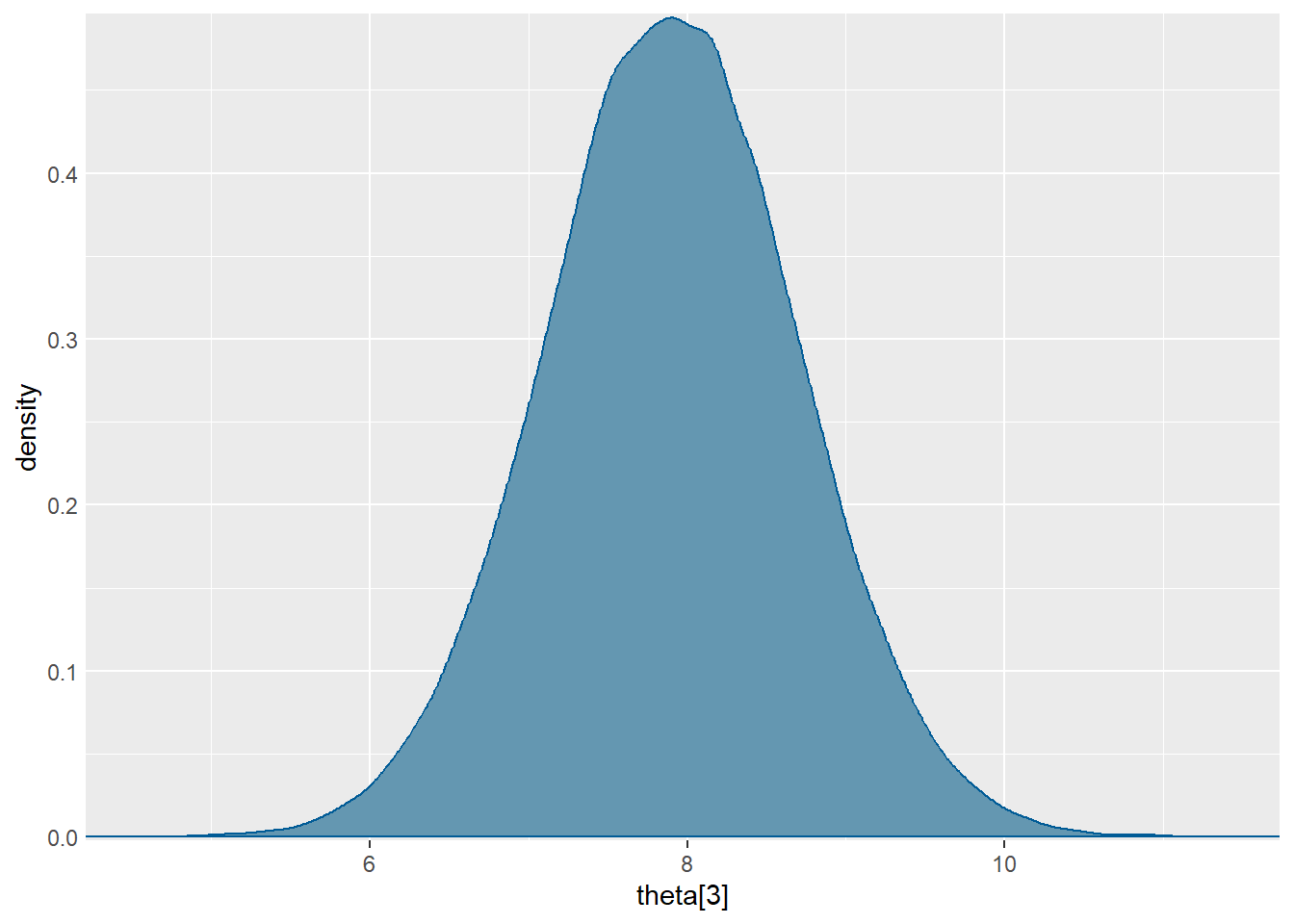

prosjeci<-c(9.464000,  7.033478,  7.953000,  6.232083, 10.765833,  6.205000,  6.132727,  7.381000)
Hijerarhijski_Bayes <- c(9.24, 7.1, 7.9, 6.4, 10.38, 6.39, 6.32, 7.41)
plot(prosjeci, Hijerarhijski_Bayes)
abline(a=0,b=1)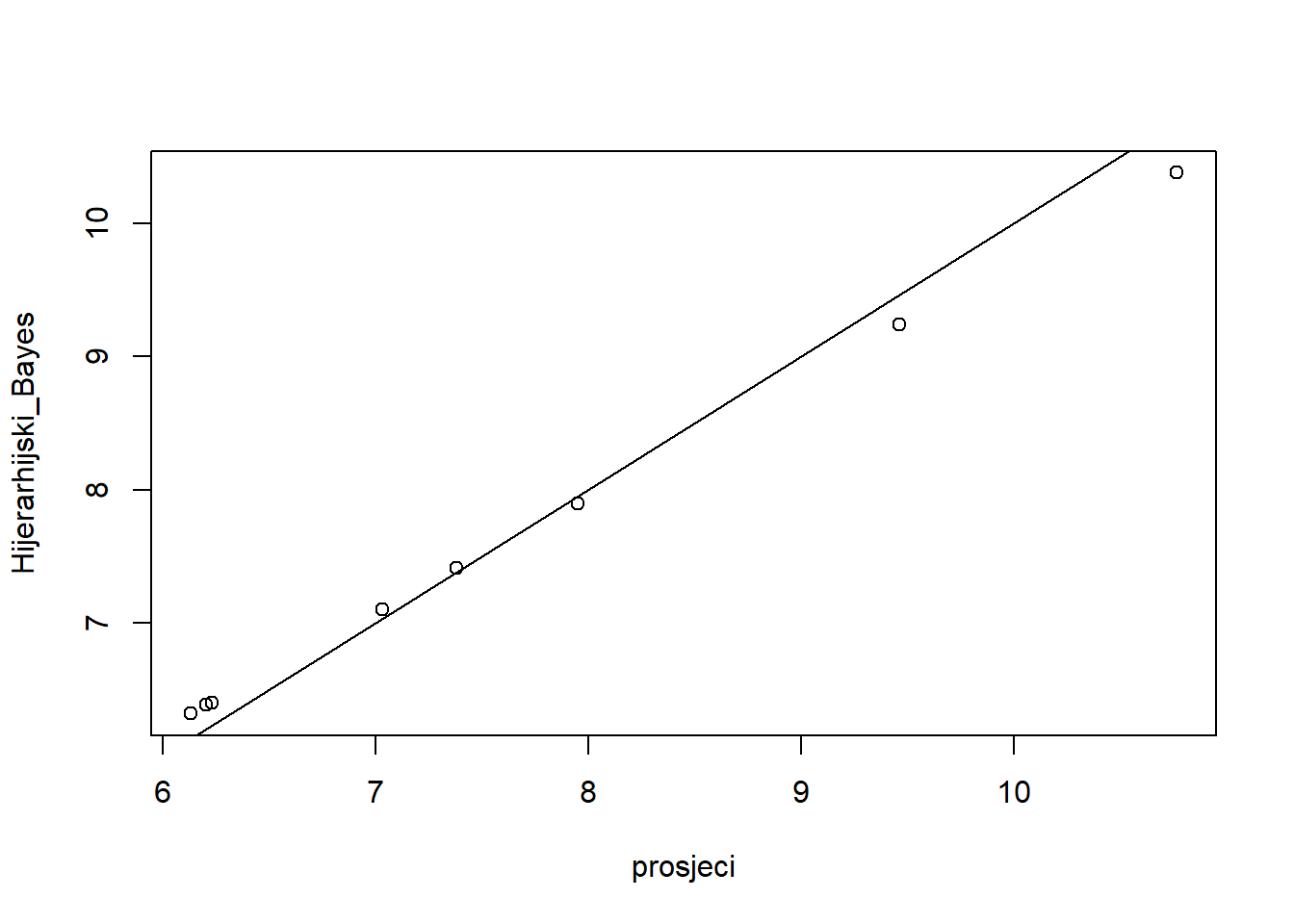

Ugrubo, možemo uočiti da Bayesovski hijerarhijski model školama s manjim prosjekom dodjeljuje veće efekte, dok onim s značajno većim većim prosjekom dodjeluje manje efekte. Iako postoje razlike, prilikom rangiranja škola prema očekivanom vremenu uloženom na zadaće one ne bi postojale.

\[P(\theta_7 < \theta_6 | \mathbb{x}_7, \mathbb{x}_6) \approx 0.52415 \]

MCMC.skole <- rstan:: extract(sim.MCMC.stan.skole)
mean(MCMC.skole$theta[,7]<MCMC.skole$theta[,6])

[1] 0.52415

\[P(\theta_7 < \min\{\theta_1, \dots, \theta_6, \theta_8\} | \mathbb{x}_1 \dots, \mathbb{x}_8) \approx 0.32285 \]

mean((MCMC.skole$theta[,7]<MCMC.skole$theta[,1]) & (MCMC.skole$theta[,7]<MCMC.skole$theta[,2]) &  (MCMC.skole$theta[,7]<MCMC.skole$theta[,3]) & (MCMC.skole$theta[,7]<MCMC.skole$theta[,4]) & (MCMC.skole$theta[,7]<MCMC.skole$theta[,5]) & (MCMC.skole$theta[,7]<MCMC.skole$theta[,6]) & (MCMC.skole$theta[,7]<MCMC.skole$theta[,8]))

[1] 0.32285