4 Vjerodostojna područja (intervali)
Za skup \(C_{\mathbb{x}}\) kažemo da je \(\alpha\)-vjerodostojno područje (uz dane podatke \(\mathbb{x}\)) za parametar \(\theta\) ako je \[P(\theta \in C_{\mathbb{x}} | \mathbb{X}=\mathbb{x}) \geq 1-\alpha.\] Specijalno, ako je \(C_{\mathbb{x}}=\left[l(\mathbb{x}), d(\mathbb{x})\right] \subset \mathbb{R}\) kažemo da se radi o \(\alpha\)-vjerodostojnom intervalu.
Za \(\alpha\)-vjerodostojno područje kažemo da je područje najveće posteriorne gustoće \(s(\mathbb{x})\) i pišemo HPD područje (od eng. highest posterior density) ako vrijedi:
- \(P(\theta \in C_{\mathbb{x}} | \mathbb{X}=\mathbb{x}) = 1-\alpha.\)
- \(\forall \theta_a \in s(\mathbb{x}), \, \theta_b \notin s(\mathbb{x})\) je \(f(\theta_a | \mathbb{x}) > f(\theta_b | \mathbb{x}).\)
Primijetimo da sve točke HPD područja imaju veću posteriornu gustoću nego točke izvan područja uz zadani \(\alpha\).
Pretopostavimo da 10 puta nezavisno bacamo novčić i da padnu dvije glave. Odredimo vjerodostojni i pouzdani interval uz \(\alpha=0.05\) za nepoznatu proporciju glava \(\theta\): - Vjerodostojnost: \(f(x | \theta)=\binom{10}{x}\theta^x \left(1-\theta\right)^{10-x}\) - Podaci: \(x=2\) - Iskoristimo konjugiranu apriornu distribuciju, odnosno pripadni Beta-Binomni model: \(f(\theta)=I_{\langle 0, 1 \rangle }(\theta) \Rightarrow\theta \sim U(0,1)\), odnosno \(\theta \sim Beta(1,1)\) - posteriorna distribucija: \(\theta | \{X=2\} \sim Beta(1+2, 1+10-2)=Beta(3,9)\)
f<-2 #podaci (frekvencija glava)
n<-10 #broj bacanja novcica
xhat<-f/n #relativna frekvencija glava
c(xhat-qnorm(0.975)*sqrt(xhat*(1-xhat)/n),xhat+qnorm(0.975)*sqrt(xhat*(1-xhat)/n)) #frekvencionisticki 95% pouzdani interval[1] -0.04791801 0.44791801Dakle, \(95\%\)-tni pouzdani interval za proporciju glava (frekvencionistički pristup) je \[\left[-0.04791801, 0.44791801\right]\]
qbeta(c(0.025,0.975),3,9) #Bayesov vjerodostojni interval[1] 0.06021773 0.51775585S druge strane, 0.05-vjerodostojni interval (Bayesov pristup) je \[\left[0.06021773, 0.51775585\right]\]
hdi(qbeta,shape1=3,shape2=9,credMass=0.95) lower upper
0.04055517 0.48372366
attr(,"credMass")
[1] 0.95Pripadni HPD (highest posterior density) interval je \[\left[0.04055517, 0.48372366\right]\]
Sljedeći kod grafički ilustrira “standardni” vjerodostojni interval i HPD interval:
curve(dbeta(x,3,9))
abline(v=qbeta(0.025,3,9),lty="dashed")
abline(v=qbeta(0.975,3,9),lty="dashed")
lines(c(qbeta(0.025,3,9),qbeta(0.975,3,9)),c(dbeta(qbeta(0.025,3,9),3,9),dbeta(qbeta(0.975,3,9),3,9)), lty="dashed")
abline(v=0.04055517 , col="red",lty="dashed")
abline(v=0.48372366 , col="red",lty="dashed")
abline(h=dbeta(0.04055517,3,9),col="red", lty="dashed")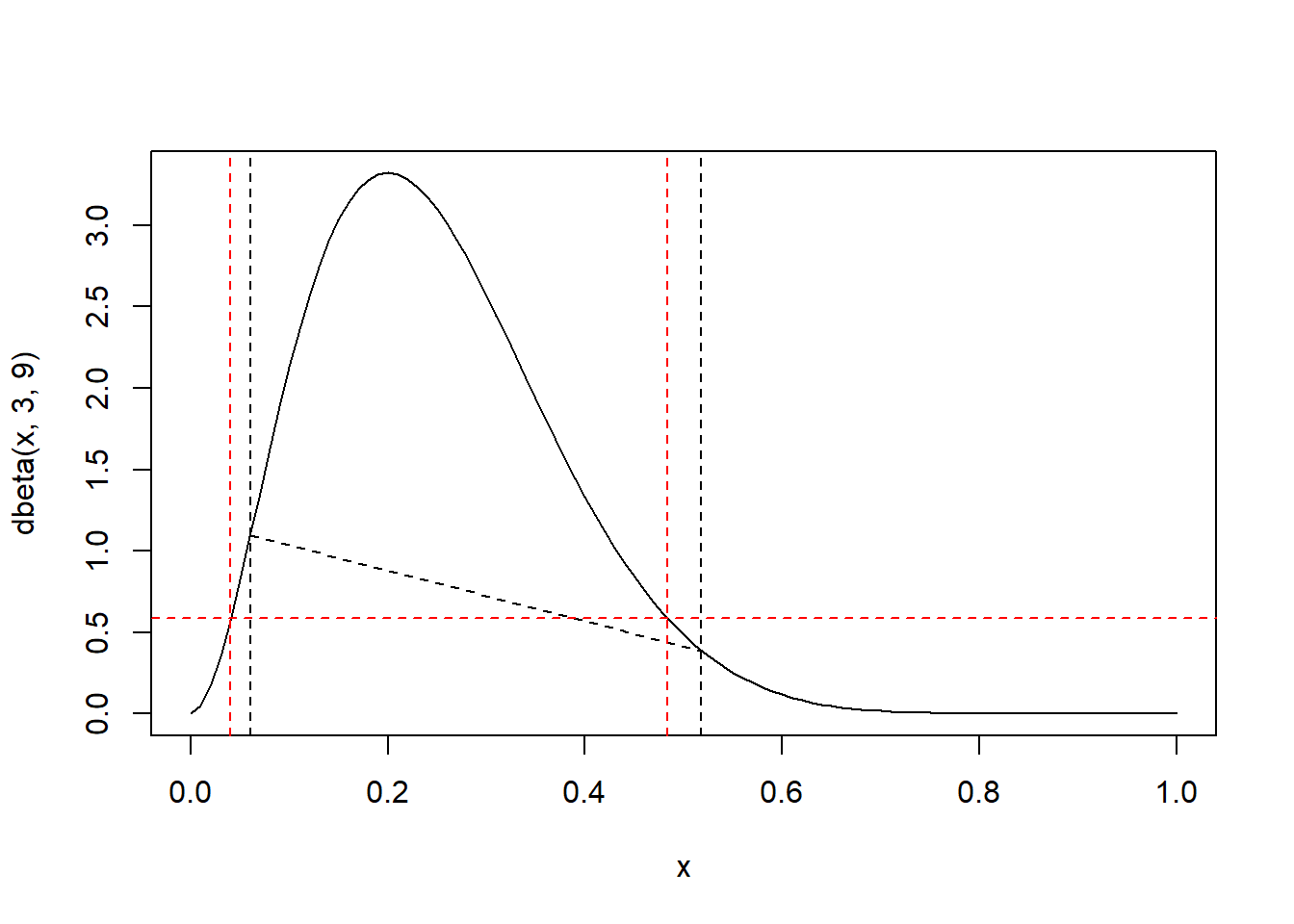
Možemo uočiti da je HPD interval uži u odnosnu na vjerodostojni interval dobiven kvantilima, pri čemu oba imaju \(95\%\) vjerojatnosti da sadrže \(\theta\).
5 Zadaci
Zadatak 5.1 Za nepoznate parametre u zadacima 3.4. - 3.7. odredite 0.05-vjerodostojne intervale standardno i korištenjem metode najveće posteriorne gustoće.
Zadatak 3.4. Posteriorna distribucija: \(\lambda | \{\mathbb{X}=\mathbb{x}\} \sim \Gamma\left(4+100, 3+63.09\right)=\Gamma\left(104, 66.09\right)\)
- “standardni” 0.05-vjerodostojni interval: \(\left[1.285755,1.890111\right]\)
qgamma(c(0.025,0.975),104,66.09)[1] 1.285755 1.890111- HPD 0.05-vjerodostojni interval: \(\left[1.276348, 1.879410\right]\)
hdi(qgamma,shape=104,rate=66.09,credMass=0.95) lower upper
1.276348 1.879410
attr(,"credMass")
[1] 0.95- Zadatak 3.5. Posteriorne distribucije:
\(\theta_1 | \mathbb{x} \sim Beta\left(\sum\limits_{i=1}^n x_i +12, 60\cdot 3 - \sum\limits_{i=1}^n x_i+3\right)= Beta\left(170, 25\right)\)
\(\theta_2 | \mathbb{y} \sim Beta\left(\sum\limits_{i=1}^n y_i +9.9875, 60\cdot 3 - \sum\limits_{i=1}^n y_i+1.7625\right)= Beta\left(170.9875, 20.7625\right)\)
"standardni" 0.05-vjerodostojni intervali:- za \(\theta_1\): \(\left[0.8215389, 0.9148389\right]\)
- za \(\theta_2\): \(\left[0.8441667, 0.9315524\right]\)
qbeta(c(0.025,0.975),170,25)[1] 0.8215389 0.9148389qbeta(c(0.025,0.975),170.9875, 20.7625)[1] 0.8441667 0.9315524HPD 0.05-vjerodostojni intervali:- za \(\theta_1\): \(\left[0.8243324, 0.9170963\right]\)
- za \(\theta_2\): \(\left[0.8471935, 0.9339220 \right]\)
hdi(qbeta,shape1=170,shape2=25,credMass=0.95) lower upper
0.8243324 0.9170963
attr(,"credMass")
[1] 0.95hdi(qbeta,shape1=170.9875,shape2=20.7625,credMass=0.95) lower upper
0.8471935 0.9339220
attr(,"credMass")
[1] 0.95Zadatak 3.6. Posteriorne distribucije:
\(\lambda_1 | \mathbb{x} \sim \Gamma\left(2+\sum\limits_{i=1}^n x_i, 1+n_1\right)= \Gamma\left(219, 112\right)\)
\(\lambda_2 | \mathbb{y} \sim \Gamma\left(2+\sum\limits_{i=1}^n y_i, 1+n_2\right)= \Gamma\left(68, 45\right)\)
"standardni" 0.05-vjerodostojni intervali:- za \(\lambda_1\): \(\left[1.704943, 2.222679\right]\)
- za \(\lambda_2\): \(\left[1.173437, 1.890836\right]\)
qgamma(c(0.025,0.975),219,112)[1] 1.704943 2.222679qgamma(c(0.025,0.975),68, 45)[1] 1.173437 1.890836HPD 0.05-vjerodostojni intervali:- za \(\lambda_1\): \(\left[1.699263, 2.216473\right]\)
- za \(\lambda_2\): \(\left[1.159872, 1.874921 \right]\)
hdi(qgamma,shape=219,rate=112,credMass=0.95) lower upper
1.699263 2.216473
attr(,"credMass")
[1] 0.95hdi(qgamma,shape=68,rate=45,credMass=0.95) lower upper
1.159872 1.874921
attr(,"credMass")
[1] 0.95Zadatak 3.7.
\(\mu_1 | \{\mathbb{X}=\mathbb{x}\} \sim \mathcal{N}(1.805,0.002)\)
\(\mu_2 | \{\mathbb{Y}=\mathbb{y}\} \sim \mathcal{N}(1.927,0.001)\)
"standardni" 0.05-vjerodostojni intervali:- za \(\mu_1\): \(\left[1.717348, 1.892652\right]\)
- za \(\mu_2\): \(\left[1.86502, 1.98898\right]\)
qnorm(c(0.025,0.975),1.805,sqrt(0.002))[1] 1.717348 1.892652qnorm(c(0.025,0.975),1.927, sqrt(0.001))[1] 1.86502 1.98898HPD 0.05-vjerodostojni intervali:- za \(\mu_1\): \(\left[1.717348, 1.892652\right]\)
- za \(\mu_2\): \(\left[1.86502, 1.98898 \right]\)
hdi(qnorm,mean=1.805,sd=sqrt(0.002),credMass=0.95) lower upper
1.717348 1.892652
attr(,"credMass")
[1] 0.95hdi(qnorm,mean=1.927,sd=sqrt(0.001),credMass=0.95) lower upper
1.86502 1.98898
attr(,"credMass")
[1] 0.95