3 O izboru apriorne distribucije

Apriornu distribuciju shvaćamo kao subjektivno mišljenje o nepoznatom parametru koje kvantificiramo vjerojatnosno kroz distribuciju.

U tom kontekstu imamo dva pristupa:

neinformativne apriorne distribucije: imaju minimalan utjecaj na posteriornu distribuciju, odnosno donesene zaključke u Bayesovskoj paradigmi
informativne apriorne distribucije: imaju ugrađeno “znanje” o parametru na temelju prethodnih istraživanja, subjektivnog mišljenja ili iskustva.

3.1 Neinformativne apriorne distribucije

Grubo ih dijelimo na sljedeće skupine:

Uniformna apriorna distribucija

Koristimo ukoliko nemamo nikakvo prethodno znanje o parametru (dodjeljujemo svim mogućim vrijednostima parametra jednake “težine”). U slučaju da je prostor parametara beskonačan (prebrojiv ili neprebrojiv) tada se radi o nepravoj apriornoj distribuciju jer to ona zapravo i nije (nije moguće normirati gustoću). Unatoč tome, možemo postaviti \(f(\theta) \propto c, \, c \in \mathbb{R}\), ali je potrebno provjeriti je li posteriorna distribucija doista distribucija, tj. je li normirana.

Jeffreyjeva apriorna distribucija

Motivirana je problemom reparametrizacije:

Ukoliko postavimo uniformnu apriornu distribuciju \(f(\theta)\), hoće li reparametrizirani parametar \(\phi=g(\theta)\) i dalje imati uniformnu apriornu distribuciju? Iz teorije vjerojatnosti znamo da uz \(g\) bijekciju, \(\phi\) ima funkciju gustoće \[f(\phi)=f(\theta)\left|\frac{d\theta}{d\phi}\right|\] što ne mora imati isti oblik kao početna distribucija.

Taj problem rješava upravo Jeffreyjeva apriorna distribucija koja se definira na temelju Fisherove informacije.

Fisherova informacija

Za fiksan parametar \(\theta\) Fisherova informacija definirana je izrazom \[I(\theta)=E_{\theta}\left[\left(\frac{d}{d\theta}\ln{p(x | \theta)}\right)^2\right]=-E_{\theta}\left[\frac{d^2}{d\theta^2}\ln{p(x | \theta)}\right],\] gdje je \(p(x | \theta)\) pripadna vjerodostojnost.

Jeffreyjev pristup odabiru apriorne distribucije omogućuje konzistentnost obzirom na reparametrizaciju:

Jeffreyjeva apriorna gustoća

Apriornu gustoću za parametar \(\theta\) definiranu sa \(f(\theta) \propto \sqrt{I(\theta)}\), gdje je \(I(\theta)\) Fisherova informacija, zovemo Jeffreyjeva apriorna gustoća.

Ovaj pristup (uz potrebne modifikacije) funkcionira i u multivarijatnom slučaju.

Apriorne distribucije maksimalne entropije

Apriorne distribucije dobivene maksimiziranjem entropije kao mjere količine informacija u parametru (veća entropija podrazumijeva manje informacija).

Referentne apriorne distribucije

Reflektiraju ideju traženja one apriorne distribucije koja je u srednjem smislu najudaljenija od posteriorne distribucije. Kao mjeru udaljenosti između distribucija koristi tzv. Kullback-Leiblerovu divergenciju. Zanimljivo je da za jednodimenzionalne parametre dobivamo istu apriornu distribuciju kao i u Jeffreyjevom pristupu, ali je generalno bolji pristup u multivarijatnom slučaju.

3.2 Informativne apriorne distribucije

Grubo ih dijelimo na dvije skupine:

one koje definiramo na temelju vlastitog subjektivnog mišljenja o parametru
konjugirane apriorne distribucije: analitički pogodne za računske manipulacije

Konjugirana apriorna gustoća

Neka je \(\mathcal{P}\) parametarska familija apriornih gustoća, a \(\mathcal{F}\) parametarska familija uzoračkih distribucija (vjerodostojnosti). Za familiju \(\mathcal{P}\) kažemo da je konjugirana u odnosu na familiju \(\mathcal{F}\) ako \[f(\theta | \mathbb{x}) \in \mathcal{P}, \quad \forall f(\cdot | \theta) \in \mathcal{F} \text{ i } f(\cdot) \in \mathcal{P}.\]

Prethodna definicija je vrlo općenita: ukoliko bismo za \(\mathcal{P}\) postavili sve distribucije, svaka distribucija bi bila konjugirana apriorna. Međutim nas zanimaju prirodne konjugirane apriorne distribucije (gustoće iz \(\mathcal{P}\) i \(\mathcal{F}\) imaju istu funkcionalnu formu).
Ukoliko koristimo konjugiranu apriornu distribuciju, posteriorna distribucija će dolaziti iz iste familije distribucija kao i apriorna.
Konjugirane apriorne distribucije omogućavaju jednostavan pristup ažuriranju podacima kroz parametre zadane familije distribucija iz koje dolazi apriorna distribucija. Većina elemenata Bayesovskog modela se jednostavno računaju i imaju jasnu interpretaciju.
Početne vrijednosti parametara apriorne distribucije obično zovemo hiperparametri, a definiramo ih na temelju znanja/mišljenja o primjerice očekivanoj vrijednosti i raspršenosti parametra.

U nastavku objašnjavamo vezu između konjugiranih apriornih distribucija i eksponencijalne familije distribucija.

Eksponencijalna familija distribucija

Za familiju distribucija \(\mathcal{F}\) kažemo da je eksponencijalna familija ukoliko se svaki njen član može zapisati u formi \[f(x | \theta)=h(x)g(\theta)e^{\Phi(\theta)^T\cdot \,u(x)},\] gdje su \(\Phi(\theta)\) i \(u(x)\) vektori jednake dimenzije kao \(\theta\), pri čemu \(\Phi(\theta)\) zovemo prirodan parametar familije \(\mathcal{F}\).

U slučaju \(j.s.u.\) uzorka \((x_1, \dots, x_n)\) iz eksponencijalne familije imamo:

vjerodostojnost: \[\begin{align*}f(\mathbb{x} | \theta)=\prod\limits_{i=1}^{n}f(x_i | \theta)&=\left[\prod\limits_{i=1}^{n}h(x_i)\right]g(\theta)^n exp\{\Phi(\theta)^T \sum_{i=1}^{n}u(x_i)\} \\ & \propto g(\theta)^n exp\{\Phi^T(\theta) t(\mathbb{x})\}, \end{align*}\] gdje je \(t(\mathbb{x})=\sum_{i=1}^{n}u(x_i)\)
Izaberemo apriornu distribuciju u obliku koji prati funkcionalnu formu vjerodostojnosti \[f(\theta)\propto g(\theta)^{\color{red}{\alpha}} e^{\Phi(\theta)^T \color{red}{\beta}},\] pri čemu su \(\alpha\) i \(\beta\) hiperparametri apriorne distribucije.
Time dobivamo posteriornu distribuciju koja je istog oblika kao apriorna ali s ažuriranim parametrima temeljem podataka kroz zbroj vrijednosti podataka \(\left(\sum\limits_{i=1}^n x_i\right)\) i broj podataka (\(n\)):

\[\begin{align*} f(\theta | \mathbb{x}) &\propto f(\mathbb{x} | \theta ) f(\theta) \\ & \propto g(\theta)^{\color{blue}{n+\alpha}} e^{\Phi(\theta)^T \color{blue}{\left(\beta + t(\mathbb{x})\right)}} \end{align*}\]

3.3 Konjugirani modeli

Na temelju ideje konjugirane apriorne distribucije izdvajamo najosnovije i najčešće korištene konjugirane modele.

3.3.1 Gama-Poissonov model

Parametar od interesa	\(\lambda>0\) - očekivana vrijednost brojača
Vjerodostojnost	\(f(x \| \lambda)= \frac{\lambda^x e^{-\lambda}}{x!}I_{\mathbb{N}_0}(x)\)
Apriorna distribucija	\(\lambda \sim \Gamma(\alpha, \beta), \quad \alpha>0, \beta >0\) hiperparametri
Posteriorna distribucija	\(\lambda \| \{\mathbb{X}=\mathbb{x}\}\sim \Gamma(\alpha+n \bar{x}_n, \beta+n)\)
Posteriorno očekivanje	\(E[\lambda \| \mathbb{X}=\mathbb{x}]=\frac{\alpha+n \bar{x}_n}{\beta + n}\)
Posteriorna varijanca	\(Var[\lambda \| \mathbb{X}=\mathbb{x}]=\frac{\alpha+n \bar{x}_n}{\left(\beta + n\right)^2}\)
Posteriorni medijan	nema zatvoreni oblik
Mod	\(\frac{\alpha+n-1}{\beta+n\bar{x}_n}\)
Apriorna prediktivna distribucija	\(X \sim Neg-Bin\left(\alpha, \beta\right)\)
Posteriorna prediktivna distribucija	\(X_{n+1} \| X_1=x_1, \dots, X_n=x_n \sim Neg-Bin\left(\alpha+n \bar{x}_n, \beta+n\right)\)

Posteriorna distribucija je kompromis između podataka i apriorne distribucije (početnog subjektivnog uvjerenja o parametru): \[E[\lambda |\mathbb{X}=\mathbb{x}]=\overbrace{\frac{\beta}{\beta+n}}^\text{težina}\cdot\underbrace{\frac{\alpha}{\beta}}_\text{apriorno čekivanje}+\overbrace{\frac{n}{\beta+n}}^\text{težina} \cdot\underbrace{\bar{x}_n}_\text{aritmetička sredina}\] Uočimo:

ako je \(n >> \beta\): \[E[\lambda |\mathbb{X}=\mathbb{x}] \approx \bar{x}_n, \quad Var[\lambda |\mathbb{X}=\mathbb{x}] \approx \frac{\bar{x}_n}{n}.\]
ako je \(\beta >> n\): \[E[\lambda |\mathbb{X}=\mathbb{x}] \approx \frac{\alpha}{\beta}.\]
Interpretacija hiperparametara: \(\beta\) - broj apriornih “podataka”, \(\alpha\) - suma \(\beta\) apriornih “podataka”.

3.3.2 Beta-Binomni model

Parametar od interesa	\(\theta \in \langle 0,1 \rangle\) - proporcija uspjeha
Vjerodostojnost	\(f(x \| \theta)= \binom{m}{x}\theta^x \left(1-\theta\right)^{m-x}I_{\{0,1,\dots, n\}}(x)\)
Apriorna distribucija	\(\theta \sim Beta(\alpha, \beta), \quad \alpha>0, \beta >0\) hiperparametri
Posteriorna distribucija	\(\theta \| \{\mathbb{X}=\mathbb{x}\}\sim Beta(\alpha+n \bar{x}_n, \beta+mn-n \bar{x}_n)\)
Posteriorno očekivanje	\(E[\theta\| \mathbb{X}=\mathbb{x}]=\frac{\alpha+n \bar{x}_n }{\alpha+\beta+mn}\)
Posteriorna varijanca	\(Var[\theta \| \mathbb{X}=\mathbb{x}]=\frac{\left(\alpha+n \bar{x}_n\right)\left(\beta+mn-n\bar{x}_n\right)}{\left(\alpha+\beta+mn\right)^2 \left(\alpha+\beta+mn+1\right)}\)
Posteriorni medijan	nema zatvoreni oblik
Posteriorni Mod	\(\frac{\alpha+n\bar{x}_n-1}{\alpha+\beta+nm-2}\)
Apriorna prediktivna distribucija	\(X \sim Beta-Bin\left(m,\alpha, \beta\right)\)
Posteriorna prediktivna distribucija	\(X_{n+1} \| X_1=x_1, \dots, X_n=x_n \sim Beta-Bin\left(m,\alpha+n \bar{x}_n, \beta+nm-n\bar{x}_n\right)\)

Posteriorna distribucija je kompromis između podataka i apriorne distribucije (početnog subjektivnog uvjerenja o parametru): \[E[\theta |\mathbb{X}=\mathbb{x}]=\overbrace{\frac{\alpha+\beta}{\alpha+\beta+nm}}^\text{težina}\cdot\underbrace{\frac{\alpha}{\alpha+\beta}}_\text{apriorno čekivanje}+\overbrace{\frac{nm}{\alpha+\beta+nm}}^\text{težina} \cdot\underbrace{\frac{\bar{x}_n}{m}}_\text{MLE procjenitelj proporcije}\] Uočimo:

ako je \(nm >> \alpha+\beta\): \[E[\theta |\mathbb{X}=\mathbb{x}] \approx \frac{\bar{x}_n}{m}, \quad Var[\theta |\mathbb{X}=\mathbb{x}] \approx \frac{1}{nm}\cdot \frac{\bar{x}_n}{m}\cdot \left(1-\frac{\bar{x}_n}{m}\right).\]
ako je \(\alpha+\beta >> nm\): \[E[\theta|\mathbb{X}=\mathbb{x}] \approx \frac{\alpha}{\alpha+\beta}.\]
Interpretacija hiperparametara: \(\alpha\) - broj apriornih “uspjeha”, \(\beta\) - broj apriornih “neuspjeha”, \(\alpha+\beta\) - apriorna dimenzija “uzorka”.

3.3.3 Gama-Eksponencijalni model

Parametar od interesa	\(\lambda >0\) - stopa pojavljivanja događaja
Vjerodostojnost	\(f(x \| \lambda)= \lambda e^{-\lambda x}I_{\langle 0, \infty \rangle}(x)\)
Apriorna distribucija	\(\lambda \sim \Gamma(\alpha, \beta), \quad \alpha>0, \beta >0\) hiperparametri
Posteriorna distribucija	\(\lambda\| \{\mathbb{X}=\mathbb{x}\}\sim \Gamma(\alpha+n , \beta+n\bar{x}_n)\)
Posteriorno očekivanje	\(E[\lambda\| \mathbb{X}=\mathbb{x}]=\frac{\alpha+n }{\beta+n \bar{x}_n}\)
Posteriorna varijanca	\(Var[\lambda \| \mathbb{X}=\mathbb{x}]=\frac{\alpha+n }{\left(\beta+n \bar{x}_n\right)^2}\)
Posteriorni medijan	nema zatvoreni oblik
Posteriorni Mod	\(\frac{\alpha+n -1}{\beta+n \bar{x}_n}\)
Apriorna prediktivna distribucija	\(X \sim Lomax\left(\alpha, \beta\right)\)
Posteriorna prediktivna distribucija	\(X_{n+1} \| X_1=x_1, \dots, X_n=x_n \sim Lomax\left(\alpha+n, \beta+n\bar{x}_n\right)\)

Posteriorna distribucija je kompromis između podataka i apriorne distribucije (početnog subjektivnog uvjerenja o parametru): \[E[\lambda |\mathbb{X}=\mathbb{x}]=\overbrace{\frac{\beta}{\beta+n\bar{x}_n}}^\text{težina}\cdot\underbrace{\frac{\alpha}{\beta}}_\text{apriorno čekivanje}+\overbrace{\frac{n\bar{x}_n}{\beta+n\bar{x}_n}}^\text{težina} \cdot\underbrace{\frac{1}{\bar{x}_n}}_\text{MLE procjenitelj stope }\] Uočimo:

ako je \(n\bar{x}_n >> \beta\): \[E[\lambda |\mathbb{X}=\mathbb{x}] \approx \frac{1}{\bar{x}_n}, \quad Var[\lambda |\mathbb{X}=\mathbb{x}] \approx \frac{1}{n \bar{x}^2_n}.\]
ako je \(\beta >> n\bar{x}_n\): \[E[\lambda|\mathbb{X}=\mathbb{x}] \approx \frac{\alpha}{\beta}.\]
Interpretacija hiperparametara: \(\alpha-1\) - broj događaja u eksponencijalnom modelu, \(\beta\) - ukupno vrijeme čekanja do realizacije tih događaja.

3.3.4 Normalni model

Nepoznato očekivanje (\(\mu\)), poznata varijanca (\(\sigma^2\))

Parametar od interesa	\(\mu\in \mathbb{R}\) - očekivana vrijednost u modelu
Vjerodostojnost	\(f(x \| \mu)= \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}\)
Apriorna distribucija	\(\mu \sim \mathcal{N}(\mu_0, \sigma_0^2), \quad \mu_0 \in \mathbb{R}, \sigma^2_0 >0\) hiperparametri
Posteriorna distribucija	\(\mu \| \{\mathbb{X}=\mathbb{x}\}\sim \mathcal{N}(\mu_n, \sigma_n^2)\), gdje je \(\mu_n=\frac{\frac{\mu_0}{\sigma_0^2}+\frac{n}{\sigma^2}\bar{x}_n}{\frac{1}{\sigma^2_0}+\frac{n}{\sigma^2}}, \quad \frac{1}{\sigma^2_n}=\frac{1}{\sigma^2_0}+\frac{n}{\sigma^2}\)
Posteriorno očekivanje	\(E[\mu\| \mathbb{X}=\mathbb{x}]=\mu_n\)
Posteriorna varijanca	\(Var[\mu \| \mathbb{X}=\mathbb{x}]=\sigma^2_n\)
Posteriorni medijan	\(\mu_n\)
Posteriorni Mod	\(\mu_n\)
Apriorna prediktivna distribucija	\(X \sim \mathcal{N}\left(\mu_0, \sigma^2_0 + \sigma^2\right)\)
Posteriorna prediktivna distribucija	\(X_{n+1} \| X_1=x_1, \dots, X_n=x_n \sim \mathcal{N}\left(\mu_n,\sigma^2_n+\sigma^2\right)\)

Obično se u Bayesovskom normalnom modelu govori o preciznosti (recipročna vrijednost varijance):

\(\tau^2=1/\sigma^2\): uzoračka preciznost (koliko su podaci “blizu” parametra \(\mu\))
\(\tau^2_0=1/\sigma^2_0\): apriorna preciznost
\(\tau^2_n=1/\sigma^2_n\): posteriorna preciznost.
Uočimo da je preciznost aditivna: \(\tau^2_n=\tau^2_0+n\tau^2\) Posteriorna distribucija je kompromis između podataka i apriorne distribucije (početnog subjektivnog uvjerenja o parametru): \[E[\mu |\mathbb{X}=\mathbb{x}]=\mu_n=\overbrace{\frac{\tau^2_0}{\tau^2_0+n\tau^2}}^\text{težina}\cdot\underbrace{\mu_0}_\text{apriorno čekivanje}+\overbrace{\frac{n\tau^2}{\tau^2_0+n\tau^2}}^\text{težina} \cdot\underbrace{\bar{x}_n}_\text{aritmetička sredina podataka}\] Uočimo:
ako je \(n >> \tau^2_0/\tau^2\): \[E[\mu |\mathbb{X}=\mathbb{x}] \approx \bar{x}_n, \quad Var[\mu |\mathbb{X}=\mathbb{x}] \approx \frac{\sigma^2}{n}.\]
ako je \(\tau^2_0/\tau^2 >> n\): \[E[\mu|\mathbb{X}=\mathbb{x}] \approx \mu_0.\]
Interpretacija hiperparametara: \(\mu_0\) - očekivana apriorna vrijednost, \(1/\sigma^2_0\) - apriorna preciznost.

Nepoznata varijanca (\(\sigma^2\)), poznato očekivanje (\(\mu\))

Parametar od interesa	\(\sigma^2>0\) - varijanca u modelu
Vjerodostojnost	\(f(x \| \sigma^2)= \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}\)
Apriorna distribucija	\(\sigma^2 \sim InvGama(\frac{\nu_0}{2}, \frac{\nu_0}{2}\sigma^2_0), \quad \nu_0 >0 , \sigma^2_0 >0\) hiperparametri
Posteriorna distribucija	\(\sigma^2 \| \{\mathbb{X}=\mathbb{x}\}\sim InvGama\left(\frac{n+\nu_0}{2}, \frac{\nu_0 \sigma^2_0 + \sum_{i=1}^n (x_i-\mu)^2}{2}\right)\)

Interpretacija hiperparametara:

\(\nu_0\) - veličina apriornog “uzorka”
\(\sigma^2_0\) - uzoračka varijanca

Nepoznato očekivanje (\(\mu\)), nepoznata varijanca (\(\sigma^2\))

Parametar od interesa	\(\left(\mu,\sigma^2\right) \in \mathbb{R} \times \langle 0, +\infty \rangle\) - očekivanje i varijanca u modelu
Vjerodostojnost	\(f(x \| \mu, \sigma^2)= \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}\)
Apriorna distribucija	\(\sigma^2 \sim InvGama(\frac{\nu_0}{2}, \frac{\nu_0}{2}\sigma^2_0), \quad \nu_0 >0 , \sigma^2_0 >0\) hiperparametri \(\mu \|\sigma^2 \sim \mathcal{N}(\mu_0, \frac{\sigma^2}{k_0}), \quad \mu_0 \in \mathbb{R} , k_0 \in \mathbb{N}\) hiperparametri
Posteriorna distribucija	\(\sigma^2 \| \{\mathbb{X}=\mathbb{x}\}\sim InvGama\left(\frac{\nu_n}{2}, \frac{\nu_n}{2}\sigma^2_n\right)\), gdje je \(\nu_n=\nu_0 +n, \, k_n=k_0+n\), \(\nu_n \sigma^2_n=\nu_0 \sigma^2_0+ (n-1) s^2+\frac{k_0 n}{k_n}\left(\bar{x}_n - \mu_0\right)^2\) \(\mu \| \{\sigma^2, \mathbb{X}=\mathbb{x}\}\sim \mathcal{N}\left(\mu_n, \frac{\sigma^2}{k_n}\right)\), gdje je \(\mu_n=\frac{k_0\mu_0+n \bar{x}_n}{k_n}.\)

Interpretacija hiperparametara:

\(\nu_0\) - veličina apriornog “uzorka” za varijancu
\(\sigma^2_0\) - uzoračka varijanca
\(k_0\) - veličina apriornog “uzorka” za očekivanje
\(\mu_0\) - apriorna “uzoračka srednja vrijednost \(k_0\)”podataka” uz varijancu \(\sigma^2\).

3.4 Zadaci

Zadatak 3.1 Korištenjem veze između eksponencijalne familije i konjugiranih apriornih distribucija odredite konjugiranu apriornu distribuciju (i pripadnu posteriornu distribuciju) uz danu vjerodostojnost \[f(x | k,\theta)=\frac{k}{\theta}x^{k-1} e^{-x^k/\theta} I_{\langle 0, \infty\rangle }(x), \quad k>0, \,\theta >0\] i pretpostavku da je \(k\) zadana konstanta, a \(\theta\) nepoznati parametar.

Rješenje

\[\theta \sim InvGama\left(\alpha,\beta\right), \quad \theta |\{\mathbb{X}=\mathbb{x}\} \sim InvGamma\left(\alpha+n,\beta+\sum_{i=1}^{n}x_i^{k}\right)\]

Zadatak 3.2 Odredite neinformativnu apriornu distribuciju koja osigurava konzistentnost s obzirom na reparametrizaciju uz danu vjerodostojnost \[f(\mathbb{x} | \theta )= \prod_{i=1}^{n}\binom{m}{x_i} \theta^{\sum_{i=1}^{n}x_i} \left(1-\theta\right)^{m-\sum_{i=1}^{n}x_i}, \quad m \in \mathbb{N},\, \theta \in \langle 0,1 \rangle, \, \mathbb{x}=\left(x_1, x_2, \dots, x_n\right).\]

Rješenje

\(f(\theta) \propto \theta^{-1/2}\left(1-\theta\right)^{-1/2} I_{\langle 0, 1 \rangle}(\theta)\), tj. Jeffreyjeva apriorna distribucija je \(\theta \sim Beta(1/2, 1/2)\).

Zadatak 3.3 Odredite neinformativnu apriornu distribuciju koja osigurava konzistentnost s obzirom na reparametrizaciju uz danu vjerodostojnost \[f(\mathbb{x} | \lambda )= \frac{\lambda^{\sum\limits_{i=1}^{n}x}}{\prod\limits_{i=1}^{n}x_i!}e^{-n\lambda}, \quad \lambda >0, \quad \mathbb{x}=\left(x_1, x_2, \dots, x_n\right).\]

Rješenje

\(f(\lambda) \propto \lambda^{-1/2}I_{\langle 0, \infty \rangle}(\lambda)\), što je Jeffreyjeva (neprava) apriorna distribucija.

Zadatak 3.4 Prikupljeni su podaci o međuvremenima (mjereni u satima) između potresa u jednom gradu i zabilježeno je 100 potresa u 63.09 sati. Seizmolog smatra da je (apriorna) očekivana stopa pojavljivanja potresa 4/3 po satu, a pripadna varijabilnost (varijanca) 4/9.

Koji parametar nam je od interesa? Definirajte statistički model, odnosno pripadnu vjerodostojnost.
Definirajte prirodnu konjugiranu apriornu distribuciju i pripadnu posteriornu distribuciju. Grafički prikažite.
Koju (posteriornu) očekivanu stopu pojavljivanja potresa definira seizmolog nakon što analizira prikupljene podatke? Usporedite s apriornom stopom.
Koliko iznosi (posteriorna) vjerojatnost da je stopa pojavljivanja potresa barem 2 po satu nakon što seizmolog analizira podatke, a koliko temeljem apriornog subjektivnog mišljenja? Komentirajte.

Rješenje

Zanima nas parametar \(\lambda >0\) uz vjerodostojnost \[f\left(\mathbb{x} | \lambda\right)=\lambda^{100} e^{-\lambda \sum_{i=1}^{100}x_i}, \quad \lambda >0, \quad \mathbb{x}=(x_1, \dots, x_{100}), \] a koji predstavlja stopu pojavljivanja potresa po satu.

Apriorna distribucija: \(\lambda \sim \Gamma\left(4, 3\right)\)
Posteriorna distribucija: \(\lambda | \{\mathbb{X}=\mathbb{x}\} \sim \Gamma\left(4+100, 3+63.09\right)=\Gamma\left(104, 66.09\right)\)
Grafički prikaz:

curve(dgamma(x, 104,66.09),0, 10, ylim = c(0, 2.5),  col = 'red')
curve(dgamma(x, 4,3),add=TRUE, col = 'blue')
legend("topright", legend = c("Apriorna distribucija", "Posteriorna distribucija"), col = c("blue", "red"), pch = c(16, 16))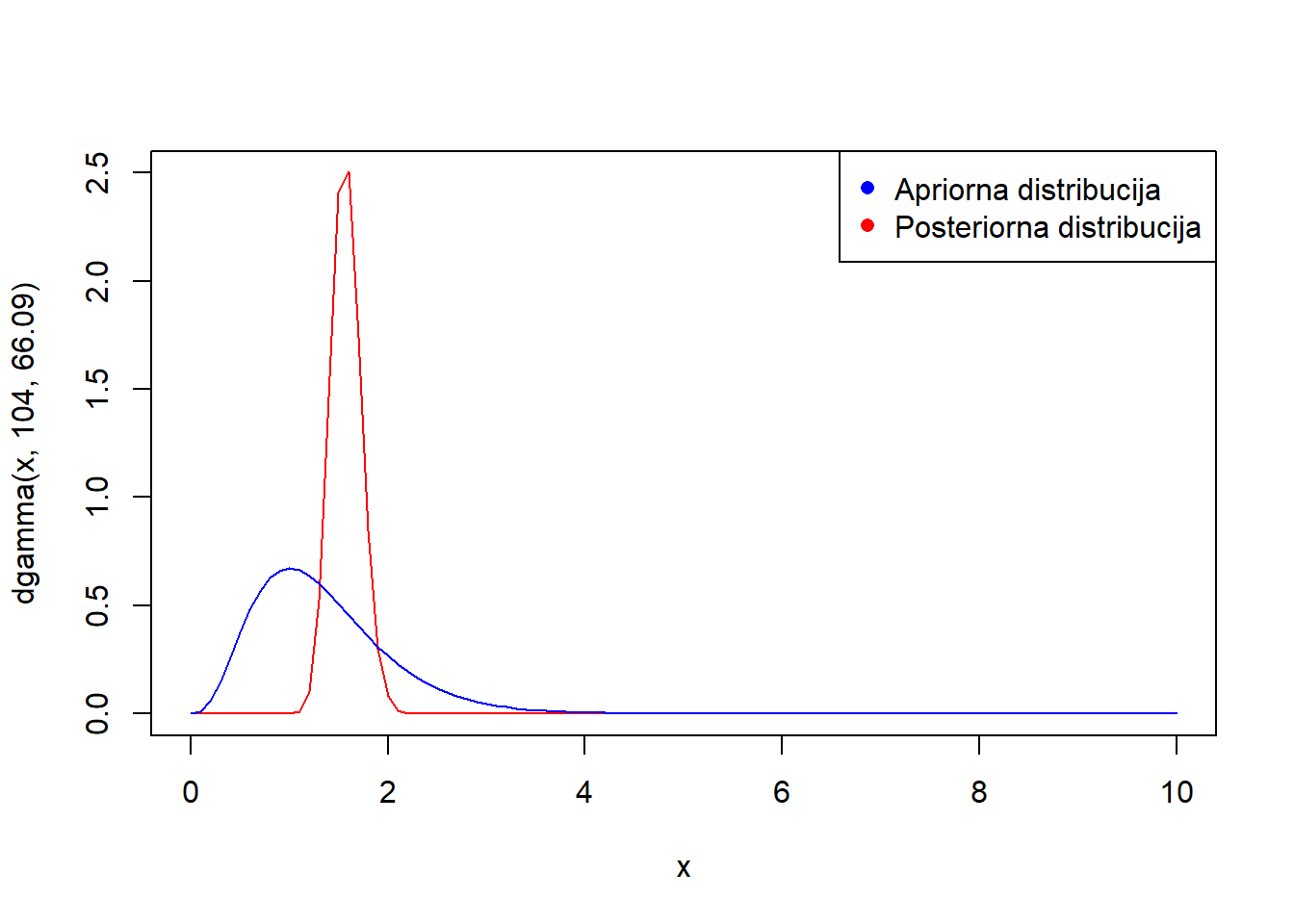

Seizmolog sada očekuje stopu pojavljivanja potresa po satu \(1.57\) uz standardnu devijaciju \(0.154\), dok je očekivana apriorna stopa bila \(1.33\) uz devijaciju \(0.67\).
\[P(\lambda >2 | \mathbb{X}=\mathbb{x}) \approx 0.00495458, \quad P(\lambda >2 ) \approx 0.1512039 \]

1-pgamma(2,104,66.09)

[1] 0.00495458

1-pgamma(2,4,3)

[1] 0.1512039

Uočavamo da se vjerojatnost pojavljivanja barem 2 potresa po satu znatno smanjila nakon što smo uzeli u obzir podatke.

Zadatak 3.5 Pretpostavimo da promatramo finale u streličarstvu u kojem sudjeluju dva ista natjecatelja u tri različite godine, pri čemu oba natjecatelja gađaju metu ukupno 60 puta, svaki puta nezavisno i s jednakom vjerojatnošću pogotka. Prikupili smo sljedeće podatke:

Natjecatelj	Prva godina	Druga godina	Treća godina
Natjecatelj 1	53	56	49
Natjecatelj 2	50	57	54

Na temelju dugogodišnjeg praćenja ovih natjecatelja očekujemo da prvi natjecatelj pogađa metu \(80\%\) puta, dok drugi \(85\%\) puta, pri čemu smatramo da je varijabilnost pogodaka (standardna devijacija) za oba natjecatelja \(1\%\).

Koji parametri su nam od interesa? Definirajte vjerodostojnost Bayesovog modela.
Odredite konjugirane apriorne i pripadne posteriorne distribucije. Prikažite grafički dobivene distribucije i komentirajte.
Koliko iznosi apriorna vjerojatnost da prvi (odn. drugi) natjecatelj ima vjerojatnost pogotka mete između \(75\%\) i \(90\%\)?
Koliko iznosi posteriorna vjerojatnost da prvi (odn. drugi) natjecatelj ima vjerojatnost pogotka mete između \(75\%\) i \(90\%\)?
Koliko iznosi posteriorna vjerojatnost da prvi natjecatelj ima veću vjerojatnost pogoditi metu nego drugi natjecatelj?
Što je vjerojatnije, da natjecatelj 1 ili natjecatelj 2 na idućem zajedničkom natjecanju ostvari barem 55 pogodaka? Grafički prikažite.

Rješenje

Zanimaju nas parametri
- \(\theta_1 \in \langle 0,1 \rangle\) vjerojatnost da natjecatelj 1 pogodi metu
- \(\theta_2 \in \langle 0,1 \rangle\) vjerojatnost da natjecatelj 2 pogodi metu Vjerodostojnosti: \[f(\mathbb{x} | \theta_1)= \prod_{i=1}^{3}\binom{60}{x_i}\theta_1^{x_i}\left(1-\theta_1\right)^{60-x_i}, \quad f(\mathbb{y} | \theta_2)= \prod_{i=1}^{3}\binom{60}{y_i}\theta_2^{y_i}\left(1-\theta_2\right)^{60-y_i},\] gdje je
- \(\mathbb{x}=(x_1, x_2, x_3)= (53, 56, 49)\), \(\mathbb{y}=(y_1, y_2, y_3)= (50, 57, 54)\).

Apriorne distribucije:

\(\theta_1 \sim Beta\left(12, 3\right)\)
\(\theta_2 \sim Beta\left(9.9875, 1.7625\right)\)

Posteriorne distribucije:

\(\theta_1 | \mathbb{x} \sim Beta\left(\sum\limits_{i=1}^n x_i +12, 60\cdot 3 - \sum\limits_{i=1}^n x_i+3\right)= Beta\left(170, 25\right)\)
\(\theta_2 | \mathbb{y} \sim Beta\left(\sum\limits_{i=1}^n y_i +9.9875, 60\cdot 3 - \sum\limits_{i=1}^n y_i+1.7625\right)= Beta\left(170.9875, 20.7625\right)\)

Grafički prikaz:

theta<-seq(from=0, to=1, by=0.01)
plot(theta, dbeta(theta,170.9875, 20.7625), type="l", col="blue", ylab="gustoća", main="Apriorna gustoća (iscrtkano) i Posteriorna gustoća (puna linija)" )
lines(theta, dbeta(theta,170,25), type="l",  col="red")
lines(theta, dbeta(theta,9.9875, 1.7625), type="l", lty="dashed", col="blue")
lines(theta, dbeta(theta,12,3), type="l", lty="dashed", col="red")
legend("topleft", legend = c("Prvi natjecatelj", "Drugi natjecatelj"), col = c("red", "blue"), pch = c(16, 16))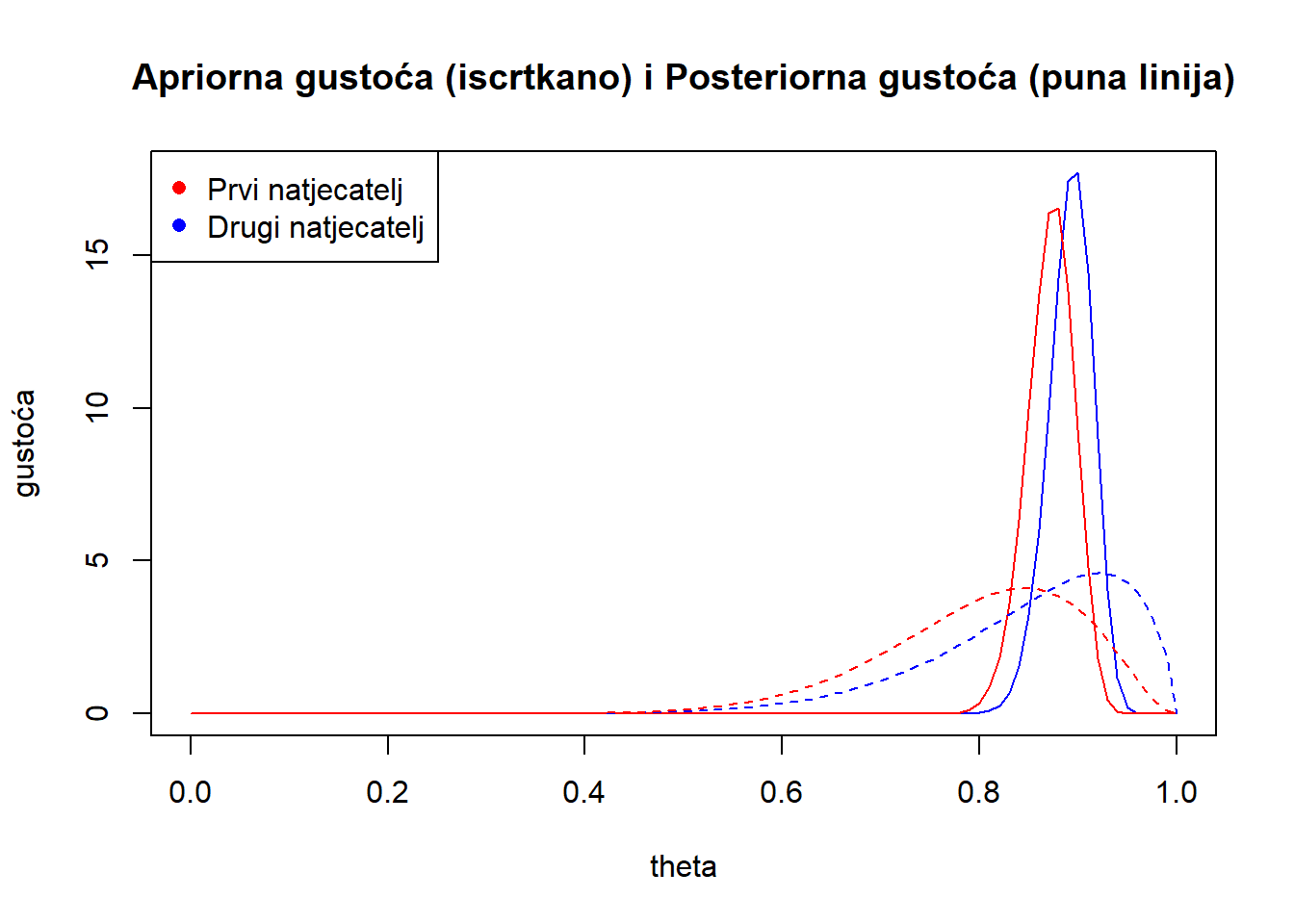

\[P(\theta_1 \in \left[0.75, 0.9\right]) \approx 0.5605124, \quad P(\theta_2 \in \left[0.75, 0.9\right]) \approx 0.4709752 \]

pbeta(0.90,12,3)-pbeta(0.75,12,3)

[1] 0.5605124

pbeta(0.90,9.9875, 1.7625)-pbeta(0.75,9.9875, 1.7625)

[1] 0.4709752

\[P(\theta_1 | \{\mathbb{X}=\mathbb{x}\} \in \left[0.75, 0.9\right]) \approx 0.886503, \quad P(\theta_2 | \mathbb{Y}=\mathbb{y} \in \left[0.75, 0.9\right]) \approx 0.6239969 \]

pbeta(0.90,170,25)-pbeta(0.75,170,25)

[1] 0.886503

pbeta(0.90,170.9875, 20.7625)-pbeta(0.75,170.9875, 20.7625)

[1] 0.6239969

Izračunajmo \[P(\theta_1 | \{\mathbb{X}=\mathbb{x}\} > \theta_2| \{\mathbb{Y}=\mathbb{y}\})\] numerički, koristeći tzv. Monte Carlo metodu. Simulirajmo 1000 realizacija slučajnih varijabli \(\theta_1 | \{\mathbb{X}=\mathbb{x}\}\) i \(\theta_2 | \{\mathbb{Y}=\mathbb{y}\}\) te izračunajmo relativnu frekvenciju događaja \(\theta_1 | \{\mathbb{X}=\mathbb{x}\} > \theta_2| \{\mathbb{Y}=\mathbb{y}\}\)

theta1 <- rbeta(1000, 170,25)
theta2 <- rbeta(1000, 170.9875, 20.7625)
mean(theta1>theta2)

[1] 0.253

Znamo da je u Beta-binomnom modelu prediktivna posteriorna distribucija Beta-binomna distribucija, tj. \[X_4 | \{\mathbb{X}=\mathbb{x}\} \sim BetaBin\left(60, 170,25\right) \Rightarrow P\left(X_4>55 | \{\mathbb{X}=\mathbb{x}\}\right) \approx 0.136\] \[ Y_4 | \{\mathbb{Y}=\mathbb{y}\} \sim BetaBin\left(60, 170.9875, 20.7625\right)\Rightarrow P\left(Y_4 >55 | \{\mathbb{Y}=\mathbb{y}\}\right) \approx 0.246\]

1-pbbinom(55,60,170,25)

[1] 0.1356478

1-pbbinom(55,60,170.9875,20.7625)

[1] 0.2458845

theta<-seq(from=0, to=60, by=1)
plot(theta, dbbinom(theta,60, 170.9875, 20.7625), type="l", col="blue", ylab="gustoća", main="Prediktivna posteriorna distribucija" )
lines(theta, dbbinom(theta,60, 170,25), type="l",  col="red")
legend("topleft", legend = c("Prvi natjecatelj", "Drugi natjecatelj"), col = c("red", "blue"), pch = c(16, 16))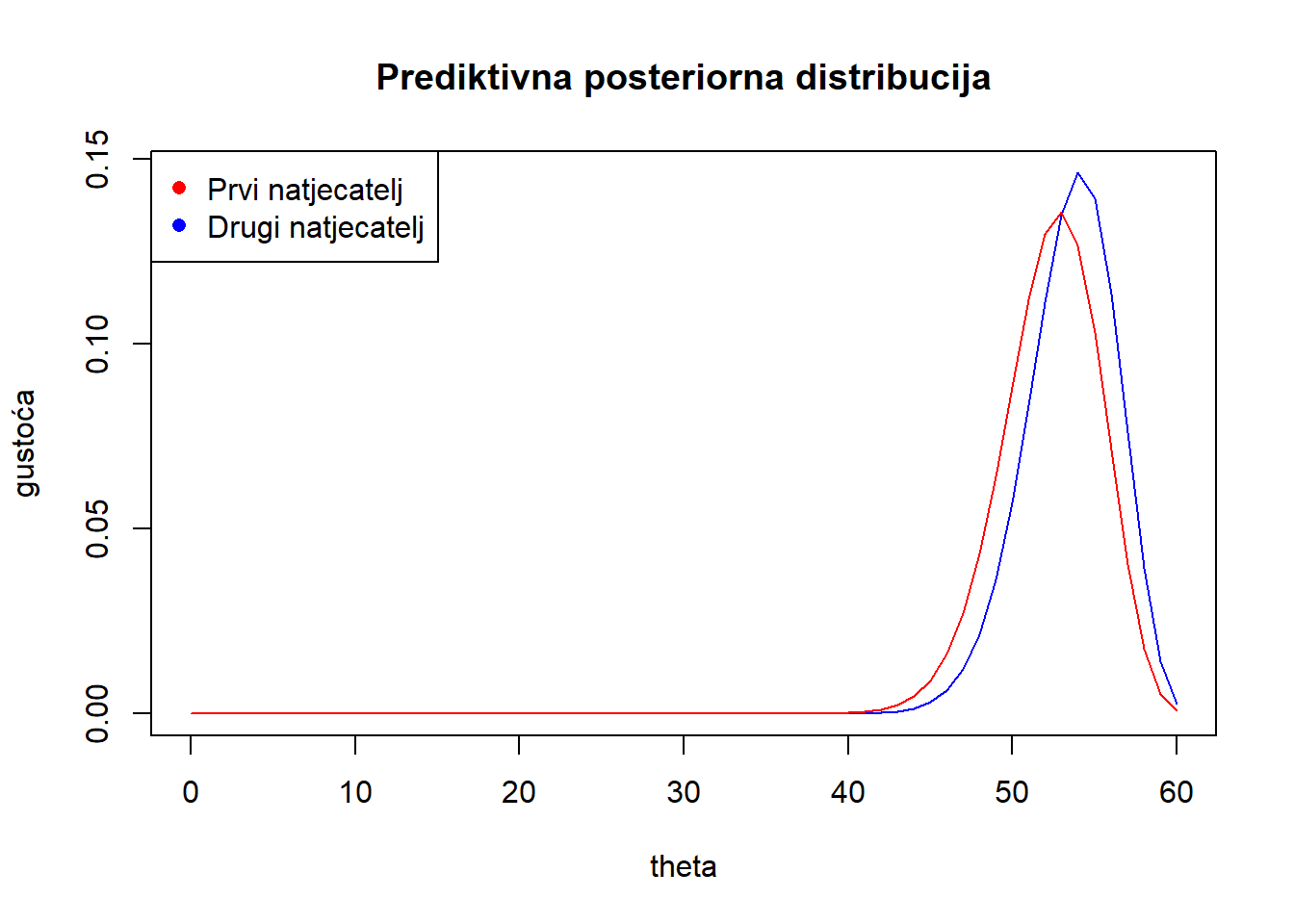

Vjerojatnije je da će na idućem natjecanju barem 55 pogodaka mete imati natjecatelj 2.

Zadatak 3.6 1990-tih prikupljeni su podaci o broju djece i stupnju obrazovanja 155 žena u SAD-u. U tijeku provedbe ankete žene su imale 40 godina. Poznato je da je 1970-tih bilo razdoblje niske stope nataliteta u SAD-u (anketirane žene su tada bile u svojim dvadesetima). U sljedećoj tablici prikazani su sumarni podaci o broju djece i stupnju obrazovanja žena:

Obrazovanje žene	Broj anketiranih žena	Ukupan broj djece svih žena
Srednja stručna sprema ili niže	111	217
Prvostupnica ili više	44	66

Koji parametri su nam od interesa? Definirajte vjerodostojnost Bayesovog modela.
Odredite konjugirane apriorne i pripadne posteriorne distribucije. Pretpostavite da apriorno očekujete dvoje djece uz varijabilnost (varijancu) 2 za obje skupine. Prikažite grafički dobivene distribucije i komentirajte.
Usporedite apriorno/posteriorno očekivanje i varijabilnost broja djece žena.
Koliko iznosi posteriorna vjerojatnost da žene s najviše srednjom stručnom spremom očekivano imaju veći broj djece od žena koje su barem prvostupnice?
Koliko iznosi posteriorna vjerojatnost da slučajno odabrana žena s najviše srednjom stručnom spremom/barem prvostupnica ima troje ili više djece? Grafički usporedite predikcije za broj djece slučajno odabranih žena koje imaju najviše srednju stručnu spremu i onih koje su barem prvostupnice. Komentirajte.

Rješenje

Zanimaju nas parametri
- \(\lambda_1 >0\) - očekivan broj djece žena s najviše srednjom stručnom spremom
- \(\lambda_2 >0\) - očekivan broj djece žena koje su barem prvostupnice

Vjerodostojnosti: \[f(\mathbb{x} | \lambda_1)= \frac{\lambda_1^{\sum\limits_{i=1}^{n}x_i}}{\prod\limits_{i=1}^{111}x_i}e^{-\lambda_1}, \quad f(\mathbb{y} | \lambda_2)= \frac{\lambda_2^{\sum\limits_{i=1}^{n}y_i}}{\prod\limits_{i=1}^{111}y_i}e^{-\lambda_2},\] gdje je - \(\mathbb{x}=(x_1, x_2, x_3, \dots, x_{111})\), \(\mathbb{y}=(y_1, y_2, \dots, y_{44})\).

Apriorne distribucije:
- \(\lambda_1 \sim \Gamma\left(2, 1\right)\)
- \(\lambda_2 \sim \Gamma\left(2, 1\right)\)
Posteriorne distribucije:
- \(\lambda_1 | \mathbb{x} \sim \Gamma\left(2+\sum\limits_{i=1}^n x_i, 1+n_1\right)= \Gamma\left(219, 112\right)\)
- \(\lambda_2 | \mathbb{y} \sim \Gamma\left(2+\sum\limits_{i=1}^n y_i, 1+n_2\right)= \Gamma\left(68, 45\right)\)

alpha <- 2
beta <- 1
n1 <- 111
n2 <- 44
x111<-217
y44<-66

#apriorno:
#obje skupine
alpha/beta #ocekivanje

[1] 2

alpha/beta^2 #varijanca

[1] 2

#posteriorno:
#zene sa najvise srednjom strucnom spremom
(alpha+x111)/(beta+n1) #ocekivanje

[1] 1.955357

(alpha+x111)/(beta+n1)^2 #varijanca

[1] 0.01745855

#zene koje su barem prvostupnice:
(alpha+y44)/(beta+n2) #ocekivanje

[1] 1.511111

(alpha+x111)/(beta+n1)^2 #varijanca

[1] 0.01745855

Izračunajmo \[P(\lambda_1 | \{\mathbb{X}=\mathbb{x}\} > \lambda_2| \{\mathbb{Y}=\mathbb{y}\})\] numerički, koristeći tzv. Monte Carlo metodu. Simulirajmo 1000 realizacija slučajnih varijabli \(\lambda_1 | \{\mathbb{X}=\mathbb{x}\}\) i \(\lambda_2 | \{\mathbb{Y}=\mathbb{y}\}\) te izračunajmo relativnu frekvenciju događaja \(\lambda_1 | \{\mathbb{X}=\mathbb{x}\} > \lambda_2| \{\mathbb{Y}=\mathbb{y}\}\)

lambda1 <- rgamma(1000, 219,112)
lambda2 <- rgamma(1000, 68,45)
mean(lambda1>lambda2)

[1] 0.969

Prema tome, vjerojatnost da žene s najviše srednjom stručnom spremom očekivano imaju veći broj djece u odnosu na žene koje su barem prvostupnice iznosi približno \(97\%\).

Znamo da je u Gama-Poissonovom modelu prediktivna posteriorna distribucija negativna-binomna distribucija, tj. \[X_{112} | \{\mathbb{X}=\mathbb{x}\} \sim NegBin\left( 219,112\right) \Rightarrow P\left(X_4\geq 3 | \{\mathbb{X}=\mathbb{x}\}\right) \approx 0.311\] \[ Y_{45} | \{\mathbb{Y}=\mathbb{y}\} \sim NegBin\left(68,45 \right)\Rightarrow P\left(Y_4 \geq 3 | \{\mathbb{Y}=\mathbb{y}\}\right) \approx 0.195\]

1-pnbinom(2,size=219,mu=219/112)

[1] 0.3112938

1-pnbinom(2,size=68,mu=68/45)

[1] 0.1952806

vjer<-c()
for(i in c(100,1000,10000,100000))
{
x112 <- rnbinom(i, size=219,mu=219/112)
y45 <- rnbinom(i, size=68,mu=68/45)
vjer<-c(vjer,mean(x112>y45))
}
vjer

[1] 0.52000 0.47200 0.48330 0.48189

Zadatak 3.7 U bazi podataka midge (iz paketa Flury) nalaze se podaci o duljini krila dviju vrsta mušica (Amerohelea fasciata (Af) i Pseudofasciata (Apf)). Pretpostavka je da mjerenja dolaze iz normalne distribucije s poznatim varijancama (\(\sigma_1^2=0.017\), \(\sigma^2_2=0.008\)). Prethodna istraživanja sugeriraju da je očekivana duljina krila za mušice \(1.9 mm\). Napomena: Baza Flury je nedostupna u najnovijoj verziji R-a, te ju možemo dohvatiti putem arhiva:

install.packages("remotes")
library(remotes)
install_version("Flury", "0.1-3")
library(Flury)

Odredite konjugiranu apriornu distribuciju i pripadnu posteriornu distribuciju za očekivanu duljinu krila mušica pojedine vrste uz korištenje činjenice da očekivana vrijednost umanjena za dvije standardne devijacije treba biti pozitivna.
Odredite Bayesov procjenitelj očekivane duljine krila mušica pojedine vrste uz apsolutnu udaljenost kao funkciju rizika.
Nakon što uzmemo podatke u obzir, koliko iznosi vjerojatnost da je očekivana duljina krila pojedine vrste mušice veća od 2 mm? Usporedite s istom vjerojatnošću prije nego uzmemo podatke u obzir.
Nakon što uzmemo u obzir podatke, koliko je vjerojatno da slučajnim odabirom jedne mušice svake vrste ustvrdimo da je mušica vrste Amerohelea fasciata veća od mušice vrste Pseudofasciata?

Rješenje

data(midge)
attach(midge)

S obzirom da je vjerodostojnost iz normalne distribucije, zaključujemo da je konjugirana apriorna distribucija normalna, tj. imamo:

\[\mu_1 \sim \mathcal{N}(1.9, 0.95^2), \quad f(x | \mu_1)=\frac{1}{\sqrt{2\pi \cdot 0.017}}e^{-\frac{\left(x-\mu_1\right)^2}{2\cdot 0.017}},\] pri čemu je varijanca apriorne distribucije dobivena temeljem zahtjeva da očekivana vrijednost umanjena za dvije standardne devijacije treba biti pozitivna: \[\mu_0 - 2 \sigma_0 >0 \Rightarrow \sigma_0 < 0.95.\] Pripadna posteriorna distribucija je

\[\mu_1 | \{\mathbb{X}=\mathbb{x}\} \sim \mathcal{N}(1.805,0.002)\] što lako dobijemo iz sljedećeg koda:

mu0.Af <- 1.9
sigma0.Af <- 0.95
sigma.Af <- sqrt(0.017)
hat.Af <- mean(Wing.Length[Species=="Af"]) 
n.Af <- length(Wing.Length[Species=="Af"])


mun.Af <- (mu0.Af/sigma0.Af^2+n.Af/sigma.Af^2*hat.Af)/(1/sigma0.Af^2+n.Af/sigma.Af^2)
mun.Af

[1] 1.804644

sigman.Af <-1/(1/sigma0.Af^2+n.Af/sigma.Af^2)
sigman.Af

[1] 0.001884944

Slično, za očekivanu duljinu krila mušice vrste Pseudofasciata imamo: \[\mu_2 \sim \mathcal{N}(1.9, 0.95^2), \quad f(y | \mu_2)=\frac{1}{\sqrt{2\pi \cdot 0.008}}e^{-\frac{\left(y-\mu_2\right)^2}{2\cdot 0.008}},\] uz pripadnu posteriornu distribuciju

\[\mu_2 | \{\mathbb{Y}=\mathbb{y}\} \sim \mathcal{N}(1.927,0.001)\]

što se lako dobije iz koda:

mu0.Apf <- 1.9
sigma0.Apf <- 0.95
sigma.Apf <- sqrt(0.008)
hat.Apf <- mean(Wing.Length[Species=="Apf"]) 
n.Apf <- length(Wing.Length[Species=="Apf"])


mun.Apf <- (mu0.Apf/sigma0.Apf^2+n.Apf/sigma.Apf^2*hat.Apf)/(1/sigma0.Apf^2+n.Apf/sigma.Apf^2)
mun.Apf

[1] 1.926627

sigman.Apf <-1/(1/sigma0.Apf^2+n.Apf/sigma.Apf^2)
sigman.Apf

[1] 0.001331366

Znamo da je Bayesov procjenitelj uz apsolutni rizik medijan posteriorne distribucije, što su u ovom slučaju isto što i pripadna očekivanja, tj.:

\[medijan\left(\mu_1 | \{\mathbb{X}=\mathbb{x}\}\right)=1.805, \quad medijan\left(\mu_2 | \{\mathbb{Y}=\mathbb{y}\}\right)=1.927.\] c) Imamo:

1-pnorm(2, 1.805, sqrt(0.002)) #posteriorna vjerojatnost Af

[1] 6.493246e-06

1-pnorm(2, 1.927,sqrt(0.001)) #posteriorna vjerojatnost Apf

[1] 0.01048671

1-pnorm(2, 1.9, 0.95) #apriorna vjerojatnost Af

[1] 0.4580835

1-pnorm(2, 1.9,0.95) #apriorna vjerojatnost Apf

[1] 0.4580835

to jest \[P(\mu_1 >2) \approx 0.46, \quad P(\mu_1 >2 | \{\mathbb{X}=\mathbb{x}\}) <0.000006\] i \[P(\mu_2 >2) \approx 0.46, \quad P(\mu_2 >2 | \{\mathbb{Y}=\mathbb{y}\}) \approx 0.01\] d) Traženu vjerojatnost odredimo temeljem posteriornih prediktivnih distribucija, tj. distribucija \[X_{10} | \{\mathbb{X}=(x_1, \dots, x_9)\} \sim \mathcal{N}(1.805,0.037), \quad Y_{7} | \{\mathbb{Y}=(y_1, \dots, y_6)\} \sim \mathcal{N}(1.927,0.009).\] Koristeći Monte Carlo aproksimaciju

vjer<-c()
for(i in c(100,1000,10000,100000,1000000))
{
x10 <- rnorm(i, 1.805,0.037)
y7 <- rnorm(i, 1.927,0.009)
vjer<-c(vjer,mean(x10>y7))
}
vjer

[1] 0.000000 0.000000 0.000300 0.000740 0.000701

za traženu vjerojatnost dobivamo

\[P(X_{10} > Y_7 | \{\mathbb{X}=(x_1, \dots, x_9), \mathbb{Y}=(y_1, \dots, y_6) \} \approx 0.0007.\]