5 Monte Carlo metode
Monte Carlo metode zasnivaju se na simuliranju/generiranju velikog broja slučajnih brojeva u svrhu dobivanja aproksimacija/numeričkih rezultata nekog problema. U kontekstu Bayesovske statistike koristimo ih u svrhu aproksimacije posteriorne distribucije ili njezinih pojedinačnih karakteristika.
Neka je \(\theta\) parametar od interesa uz zadanu vjerodostojnost \(f(x_1, \dots, x_n | \theta)\). Ideja je simulirati/generirati \(S\) nezavisnih realizacija parametra \(\theta\) iz posteriorne distribucije, tj. \[\theta^{(1)}, \dots, \theta^{(S)} \sim \text{ n.j.d. iz } f(\theta | x_1, \dots, x_n).\] Posteriornu distribuciju \(f(\theta | x_1, \dots, x_n )\) možemo aproksimirati empirijskom distribucijom uzorka \(\{\theta^{(1)}, \dots, \theta^{(S)}\}\).
Neka je \(\theta^{(1)}, \dots, \theta^{(S)} \sim \text{ n.j.d. iz } p(\theta | x_1, \dots, x_n).\) Empirijska distribucija uzorka \(\{\theta^{(1)}, \dots, \theta^{(S)}\}\) naziva se Monte Carlo aproksimacija posteriorne distribucije \(f(\theta | x_1, \dots, x_n)\).
Koristeći Monte Carlo metodu možemo aproksimirati razne numeričke karakteristike nepoznatog parametra \(\theta\) (kao sl. varijable). Naime, prema jakom zakonu velikih brojeva za (gotovo svaku) funkciju \(g\) vrijedi: \[\frac{1}{S}\sum_{s=1}^{S} g(\theta^{(s)}) \to E[g(\theta) | X_1=x_1, \dots, X_n=x_n ], \quad S \to \infty, \quad \text{g.s.}\] Prema tome, kada \(S \to \infty\) imamo:
- \(\bar{\theta} \to E[\theta | X_1 = x_1, \dots, X_n =x_n]\)
- \(\hat{\sigma}^2=\frac{1}{S-1}\sum\limits_{s=1}^{S} \left(\theta^{(s)}-\bar{\theta}\right)^2 \to Var[\theta | X_1 = x_1, \dots , X_n = x_n]\)
- \(\frac{1}{S}\sum\limits_{s=1}^{S} I_{\{\theta^{(s)}\leq c\}} \to P\left(\theta \leq c | X_1 = x_1, \dots, X_n = x_n\right).\)
- empirijska distribucija od \(\{\theta^{(1)}, \dots, \theta^{(S)}\} \to f(\theta | x_1, \dots, x_n).\)
- \(medijan(\theta^{(1)}, \dots, \theta^{(S)}) \to medijan(\theta)\)
- p-kvantil od \(\{\theta^{(1)}, \dots, \theta^{(S)}\} \to \theta_p\).
Kod Monte Carlo aproksimacija najveći je problem znati je li došlo do konvergencije, odnosno jesmo li generirali dovoljno slučajnih brojeva (dovoljno velik \(S\)). U tu svrhu često se koriste grafički prikazi kojim možemo dobiti uvid u konvergenciju.
Promotrimo problem konvergencije Monte-Carlo aproksimacija u kontekstu aproksimacije posteriornog očekivanja. Prema centralnom graničnom teoremu imamo: \[\frac{\bar{\theta}-E[\theta | X_1 = x_1, \dots, X_n = X_n]}{\sqrt{Var[\theta | X_1 = x_1, \dots, X_n = X_n]/S}} \Rightarrow \mathcal{N}(0,1), \quad S \to \infty. \] Uzevši u obzir navedeno, aproksimativni 95\(\%\)-tni Monte Carlo pouzdani interval za posteriorno očekivanje je \[\left[\bar{\theta}-2\sqrt{\hat{\sigma}^2/S}, \bar{\theta}+2\sqrt{\hat{\sigma}^2/S}\right].\] Uobičajena je praksa izabrati dovoljno veliki \(S\) tako da standardna greška (\(\sqrt{\hat{\sigma}^2/S}\)) bude manja od preciznosti do na koju želimo izvjestiti posteriorno očekivanje \(E[\theta | X_1 = x_1, \dots, X_n = X_n]\).
Pretpostavimo da smo generirali uzorak dimenzije \(S=100\) za kojeg je aproksimacija za \(Var[\theta | X_1 = x_1, \dots, X_n = X_n]/S\approx 0.025\), a želimo preciznost 0.01. Tada imamo zahtjev oblika \[2\sqrt{\hat{\sigma}^2/S}< 0.01 \Rightarrow S>1000.\] Prema tome trebali bismo napraviti Monte Carlo aproksimaciju na temelju barem \(S=1000\) simuliranih vrijednosti kako bismo imali pouzdanost \(0.01\) s velikom vjerojatnošću.
5.1 Posteriorno zaključivanje za proizvoljne funkcije parametra
Pretpostavimo da nas zanima statističko zaključivanje o \(g(\theta)\) umjesto originalnog parametra \(\theta\). Monte Carlo metode nam to jednostavno pružaju kroz sljedeći postupak:
- generiraj \(\theta^{(1)} \sim f(\theta | x_1, \dots, x_n)\), izračunaj \(\gamma^{(1)}=g(\theta^{(1)})\)
- generiraj \(\theta^{(2)} \sim f(\theta | x_1, \dots, x_n)\), izračunaj \(\gamma^{(2)}=g(\theta^{(2)})\)
\(\quad \vdots\)
- generiraj \(\theta^{(S)} \sim f(\theta | x_1, \dots, x_n)\), izračunaj \(\gamma^{(S)}=g(\theta^{(S)})\)
Tako generirani uzorak \(\{\gamma^{(1)}, \dots \gamma^{(S)}\}\) sastoji se od \(S\) nezavisnih realizacije iz \(f(\gamma | x_1, \dots, x_n)\) (iz posteriorne distribucije u terminu \(\gamma=g(\theta)\)).
Sada slično kao u prethodnom poglavlju, za \(S \to \infty\) imamo:
- \(\bar{\gamma}=\frac{1}{S} \sum_{s=1}^{S} \gamma^{(s)} \to E[\gamma | X=x_1, \dots X=x_n]\)
- \(\hat{\sigma}^2=\frac{1}{S-1}\sum\limits_{s=1}^{S} \left(\gamma^{(s)}-\bar{\gamma}\right)^2 \to Var[\gamma | X_1 = x_1, \dots , X_n = x_n]\)
- empirijska distribucija od \(\{\gamma^{(1)}, \dots, \gamma^{(S)}\} \to f(\gamma| x_1, \dots, x_n)\)
\(\quad \dots\)
U Binomnom modelu \(B(n, \theta)\) mogu nas zanimati logaritmirane šanse, tj.\(\ln{\frac{\theta}{1-\theta}}\), umjesto originalnog parametra vjerojatnosti \(\theta\). U tom kontekstu želimo zaključivati o \(\gamma=g(\theta)=\ln{\frac{\theta}{1-\theta}}\). Uočimo da je \(\theta \in \langle 0,1 \rangle\), a \(\gamma \in \mathbb{R}\).
5.2 Monte Carlo Markovljevi lanci
5.2.1 Metropolis-Hastings algoritam
U kontekstu Bayesovske statistike ovaj algoritam se koristi u svrhu aproksimacije posteriorne distribucije, a onda Monte Carlo metodama aproksimiramo i sve druge numeričke karakteristike posteriorne distribucije.
Algoritam se bazira na iterativnom generiranju vrijednosti iz posteriorne distribucije korištenjem Markovljevih lanaca, a potom se koristi empirijska distribucija generiranih vrijednosti kao aproksimacija posteriorne distribucije. Iz gore navedenih razloga Metropolis-Hastings algoritam spada u MCMC metode (Markov Chain Monte Carlo).
U svakom Bayesovskom modelu zadan je parametar \(\theta\), pripadna apriorna distribucija \(f(\theta)\) i vjerodostojnosti \(f(\mathbb{x} | \theta)\). To je dovoljno za aproksimaciju posteriorne distribucije \(f(\theta | \mathbb{x})\) MCMC metodom:
- Generiraj \(\theta^* \sim T(\theta | \theta^*)\)
- Izračunaj Hastingsov omjer (“acceptance rate”): \(r=a(\theta^{(s)}, a^*)=\frac{f(\theta^* | \mathbb{x}) T(\theta^{(s)} | \theta^*)}{f(\theta^{(s)} | \mathbb{x}) T(\theta^* | \theta^{(s)})}\)
- Generiraj \(U \sim \mathcal{U}(0,1)\)
- \(\theta^{(s+1)}= \left\{\begin{array}{ccl} \theta^* & , & U \leq r \\ \theta^{(s)} & , & U>r \end{array} \right.\)
Teorem 5.1 Niz \((\theta^{(1)}, \theta^{(2)}, \dots , \theta^{(s)}, \dots)\) konstruiran Metropolis Hastings algoritmom je (reverzibilan) Markovljev lanac sa stacionarnom distribucijom \(f(\theta | \mathbb{x})\).
Više informacija o teoretskom aspektu algoritma (kao i dokaz prethodnog teorema) moguće je pronaći u knjigama Hoff (2009) i Dobrow (2016).
Primijetimo da u koraku 2. za izračun Hastingsovog omjera nije potrebno znati normalizacijsku konstantu posteriorne distribucije jer se ona u omjeru pokrati.
Usporedba \(U\) i \(r\) u koraku 4. se često radi na logaritamskoj skali radi numeričke stabilnosti algoritma.
U slučaju da koristimo simetričnu distribuciju kandidat, tj. ukoliko vrijedi \[T(\theta^{(a)} | \theta^{(b)})=T(\theta^{(b)} | \theta^{(a)})\]
algoritam se specijalno zove Metropolis algoritam, a izračun Hastingsovog omjera se svodi na \[r=a(\theta^{(s)}, a^*)=\frac{f(x|\theta^*)f(\theta^*) }{f(x|\theta^{(s)})f(\theta^{(s)})}.\] Za kandidat (simetričnu) distribuciju često koristimo:
\(T(\theta^* | \theta^{(s)}) \sim \mathcal{U}(\theta^{(s)}-\delta, \theta^{(s)}+\delta)\)
\(T(\theta^* | \theta^{(s)}) \sim \mathcal{N}(\theta^{(s)}, \delta^2)\) gdje je \(\delta>0\) parametar kojeg treba birati tako da algoritam bude efikasan (\(r\) između \(20\%\) i \(50\%\)).
Efikasnost algoritma ponajviše ovisi o izboru početne vrijednosti i distribucije kandidata.
S obzirom da Metropolis-Hastings algoritam generira niz vrijednosti \(\{\theta^{(1)}, \theta^{(2)}, \dots , \theta^{(s)}, \dots\}\) koje su zavisne koristimo pravilo sagorijevanja, tj. “burn in period”:
- Izvršavaj algoritam do iteracije B za koju je Markovljev lanac postigao stacionarnost
- Izvršavaj algoritam dodatnih S puta
- Odbaci \(\{\theta^{(1)}, \theta^{(2)}, \dots , \theta^{(B)}\}\) i koristi empirijsku distribuciju od \(\{\theta^{(B+1)}, \theta^{(2)}, \dots , \theta^{(B+S)}\}\) kao aproksimaciju za \(f(\theta | \mathbb{x})\).
trials <- 1000000
simlist <- numeric(trials)
state <- 0
for (i in 2:trials) {
prop <- runif(1, state-1,state+1)
acc <- exp(-(prop^2-state^2)/2)
if (runif(1) < acc) state <- prop
simlist[i] <- state
}
hist(simlist,xlab="",main="",prob=T)
curve(dnorm(x),-4,4,add=T)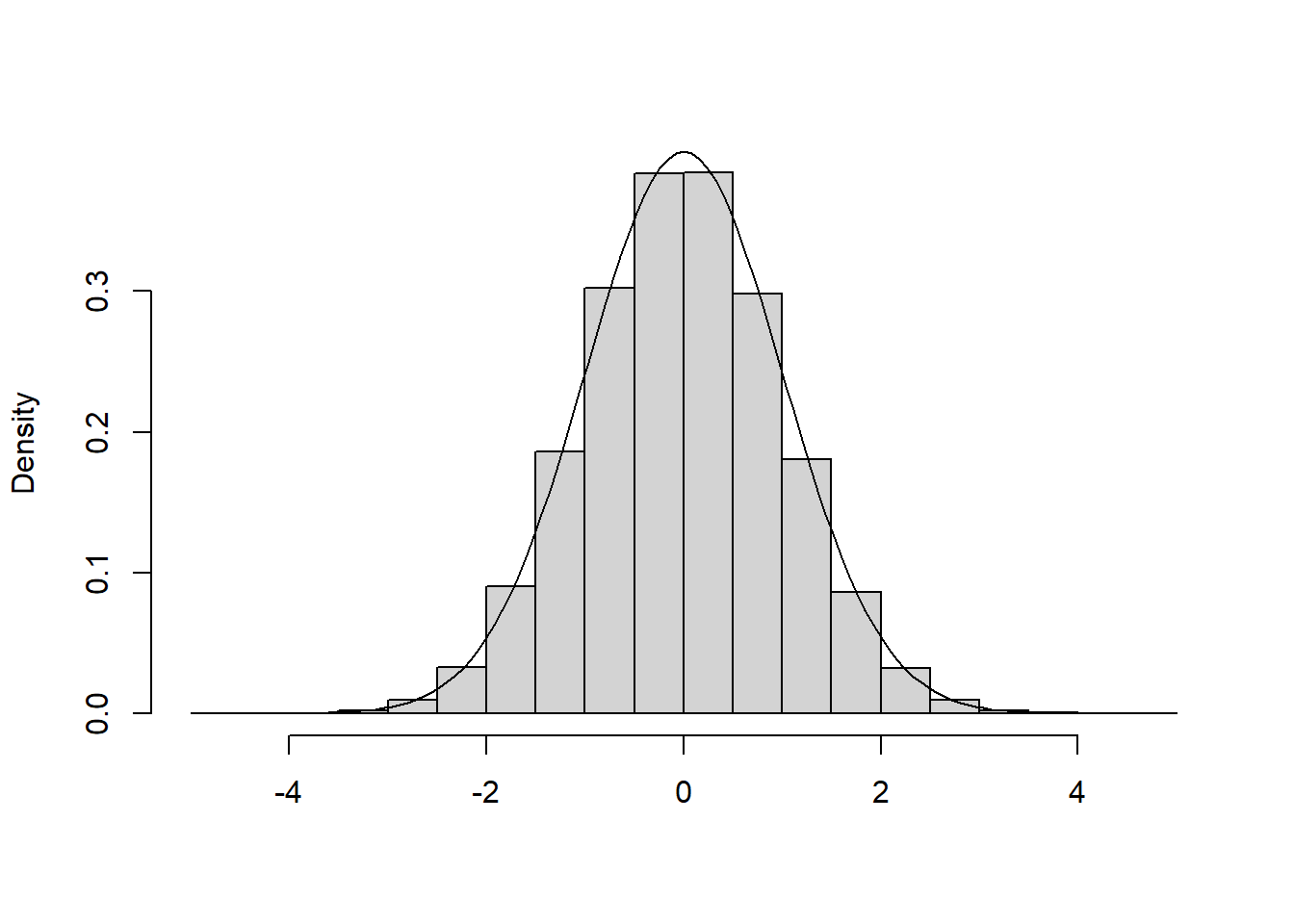
S <- 10000
sigma2<-1
mu0 <-5
sigma.02<-10
mu <- 0
delta2 <- 2
x <- c(9.37, 10.18, 9.16, 11.6, 10.33)
sim.post.mu <- NULL
for(s in 1:S)
{mu.star<-rnorm(1,mu, sqrt(delta2))
log.r <- (sum(dnorm(x,mu.star, sqrt(sigma2), log=TRUE))+dnorm(mu.star,mu0, sqrt(sigma.02), log=TRUE))-
(sum(dnorm(x,mu, sqrt(sigma2), log=TRUE))+dnorm(mu,mu0, sqrt(sigma.02), log=TRUE))
if (log(runif(1)) < log.r) {mu <-mu.star}
sim.post.mu <-c(sim.post.mu, mu)
}
plot(density(sim.post.mu), col="blue")
curve(dnorm(x,10.03, 0.44), add=T, col="red")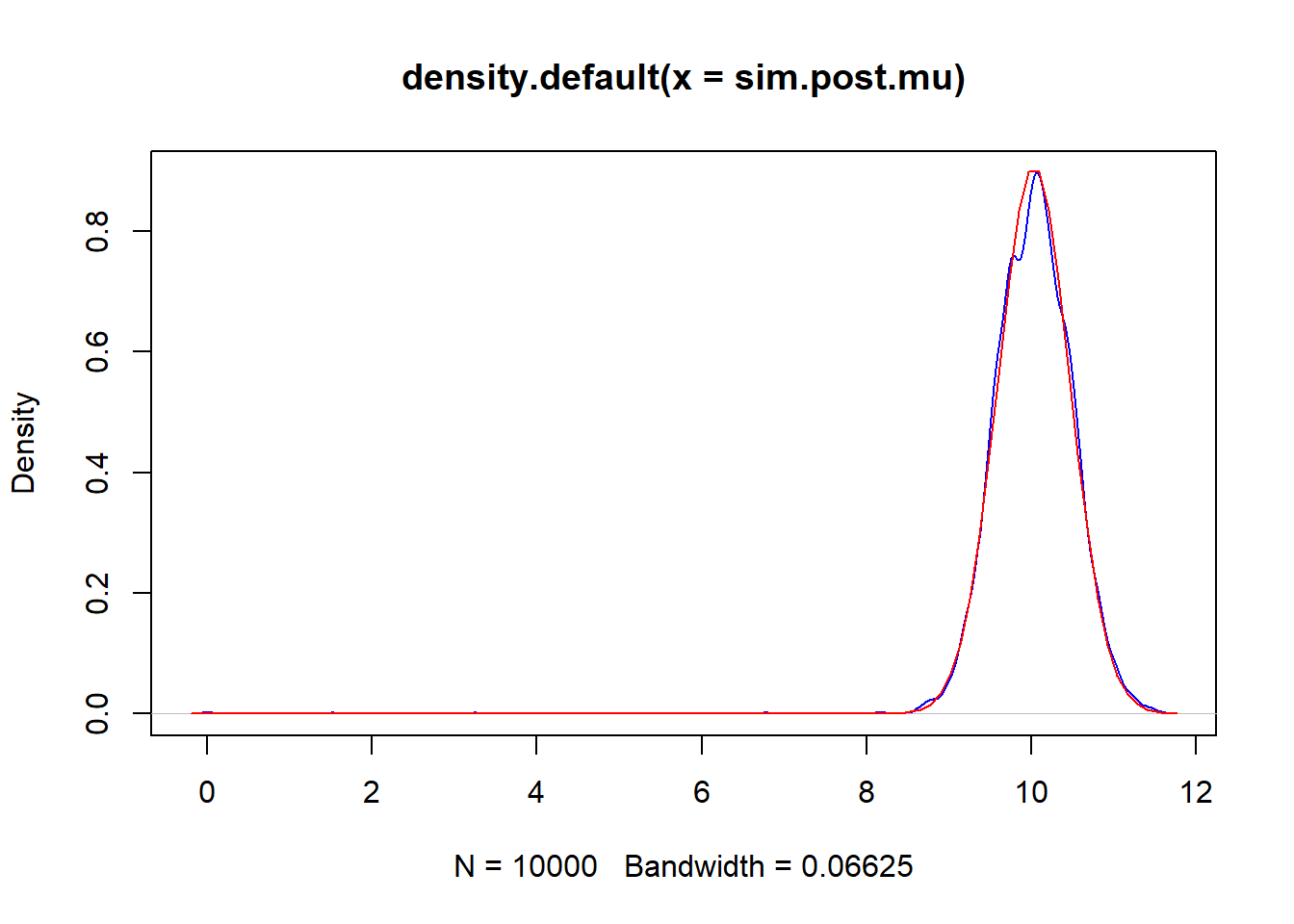
plot(ts(sim.post.mu), xlab="Iteracija")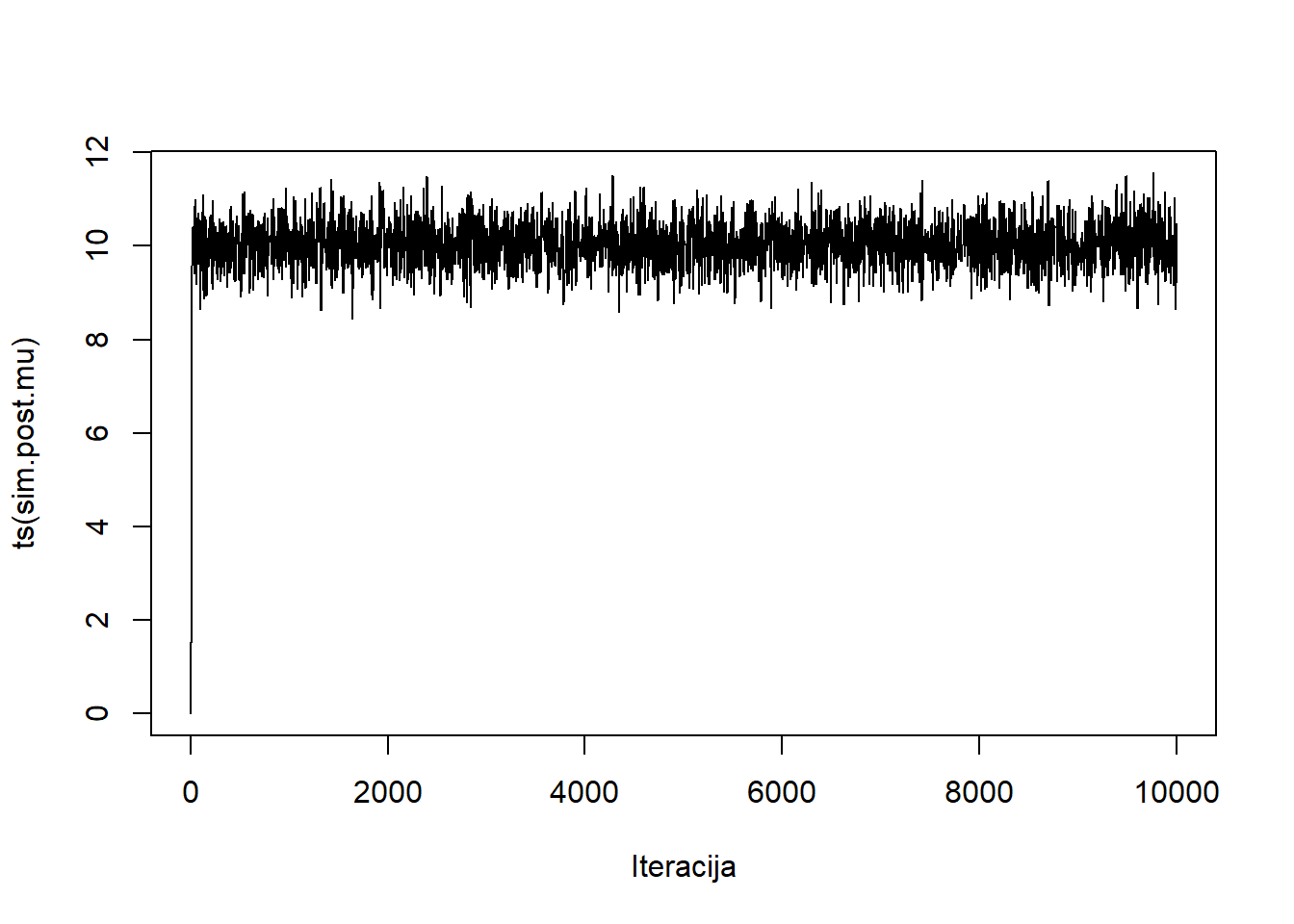
5.2.2 Gibbsovo uzorkovanje
Gibbsovo uzorkovanje je specijalizirana varijanta Metropolis Hastings algoritma koja se koristi u slučaju višedimenzionalnog parametra.
Pretpostavimo da je parametar od interesa \(p\) dimenzionalni vektor \(\phi=\left(\phi_1, \dots \phi_p\right)\) uz vjerodostojnost \(f(\mathbb{x} | \phi)\) i apriornu distribuciju \(f(\phi)\).
Algoritam se svodi na iterativno generiranje jednodimenzonalnih komponenti parametra \(\phi_k\) iz uvjetne distribucije \(f(\phi_k | \phi_1, \dots, \phi_p, \mathbb{x})\) uz poznate ostale vrijednosti komponenti parametra i podatke. Pri tome se uvijek koriste zadnje generirane vrijednosti komponenti parametra.
Izaberi početnu vrijednost parametra \(\phi^{(0)}=\left(\phi^{(0)}_1, \dots, \phi^{(0)}_p\right)\).
Generiraj \(\phi^{(s)}\) iz \(\phi^{(s-1)}\) na sljedeći način:
2.1. Generiraj \(\phi^{(s)}_1 \sim f(\phi_1 | \phi^{(s-1)}_2, \phi^{(s-1)}_3. \dots, \phi^{(s-1)}_p, \mathbb{x})\)
2.2. Generiraj \(\phi^{(s)}_2 \sim f(\phi_2 | \phi^{(s)}_1, \phi^{(s-1)}_3. \dots, \phi^{(s-1)}_p, \mathbb{x})\)
\(\dots\)
2.p. Generiraj \(\phi^{(s)}_p \sim f(\phi_2 | \phi^{(s)}_1, \phi^{(s)}_2. \dots, \phi^{(s)}_{p-1}, \mathbb{x})\)
Više informacija o teoretskom aspektu algoritma (kao i dokaz prethodnog teorema) moguće je pronaći u knjigama Hoff (2009) i Dobrow (2016).
Efikasnost Gibbsovog uzorkovanja ima naslijeđene probleme kao i ostale MCMC metode kao posljedica činjenice da se radi o specifičnoj verziji Metropolis Hastings algoritmu.
Gibbsovo uzorkovanje podrazumijeva da uvjetne distribucije jednodimenzionalnih komponenti parametra uz ostale poznate vrijednosti znamo (vidi korak 2. algoritma). Ukoliko pak iste ne znamo, mogli bismo za svaku od njih provesti Metropolis Hastings algoritam (“Metropolis with Gibbs”), međutim to može smanjujiti efikasnost i brzinu konvergencije algoritma te povećati osjetljivost na početnu vrijednost.
- MC metode oslanjaju se na jaki zakon velikih brojeva kako bi opravdali korištenje empirijske distribucije generiranih vrijednosti u svrhu aproksimacije posteriorne distribucije
- MCMC metode oslanjanju se na ergodski teorem za Markovljeve lance (svojevrsna generalizacija JZVB u slučaju Markovljevih lanaca) kako bi donijeli zaključke:
- \(P(\phi^{(s)} \in A) \to \int_{A} f(\phi | \mathbb{x}) d \phi, \quad S \to \infty\)
- \(\frac{1}{S}\sum\limits_{s=1}^{S}g(\phi^{(s)}) \to E[g(\phi) | \mathbb{X}=\mathbb{x}]=\int g(\phi) f(\phi | \mathbb{x})d\phi, \quad S \to \infty\)
Više o Ergodskom teoremu za Markovljeve lanci moguće je pronaći u knjizi Dobrow (2016).
Imamo \((X_1, \dots, X_n)\) j.s.u. iz \(\mathcal{N}(\mu, \sigma^2)\) distribucije, gdje je \(\phi=(\mu, \sigma^2)\) nepoznati parametar. Želimo simulirati vrijednosti iz posteriorne distribucije \[f(\mu, \sigma^2 | \mathbb{x}).\] Sljedeći kod provodi Gibbsovo uzorkovanje koje možemo sažeti na idući način:
- početna vrijednost: \(\phi^{(0)}=(\mu^{(0)}, \sigma^{2(0)})=(\bar{x}_n, s^2_n)\) (početna vrijednost može biti proizvoljna, ali radi ubrzavanja algoritma dobro je birati vrijednosti koje su koncentrirane u dijelovima velike gustoće posteriorne distribucije, npr. mod)
- generiraj \(\phi^{s}\) iz \(\phi^{(s-1)}\) korištenjem uvjetnih distribucija:
- generiraj \(\mu^{(s)} \sim f(\mu | \sigma^{2(s-1)}, \mathbb{x})\) (normalni model uz poznatu varijancu)
- generiraj \(\sigma^{2(s)} \sim f(\sigma^2 | \mu^{2(s)}, \mathbb{x})\) (normalni model uz poznato očekivanje)
U konačnici dobivamo niz \(S\) parova \[\{(\mu^{(0)}, \sigma^{2(0)}), \dots, (\mu^{(S)}, \sigma^{2(S)})\}\] iz posteriorne distribucije.
Kod - Gibbsovo uzorkovanje
# Hiperparametri apriorne distribucije
mu0<-1.9 ; t20<-0.95^2
s20<-.01 ; nu0<-1
# Podaci
y<-c(1.64,1.70,1.72,1.74,1.82,1.82,1.82,1.90,2.08)
n<-length(y) ; mean.y<-mean(y) ; var.y<-var(y)
## Početne vrijednosti za Gibbsovo uzorkovanje
S<-1000
PHI<-matrix(nrow=S,ncol=2)
PHI[1,]<-phi<-c( mean.y, 1/var.y)
## Gibbsovo uzorkovanje
for(s in 2:S) {
# generiramo novi *mu* iz njegove uvjetne distribucije (normalni model s poznatom varijancom)
mun<- ( mu0/t20 + n*mean.y*phi[2] ) / ( 1/t20 + n*phi[2] )
t2n<- 1/( 1/t20 + n*phi[2] )
phi[1]<-rnorm(1, mun, sqrt(t2n) )
#generiraj novi *sigma^2* iz njegove uvjetne distribucije (normalni model s poznatim ocekivanjem )
nun<- nu0+n
s2n<- (nu0*s20 + (n-1)*var.y + n*(mean.y-phi[1])^2 ) /nun
phi[2]<- rgamma(1, nun/2, nun*s2n/2)
PHI[s,]<-phi }Radi veće efikasnosti algoritma prilikom ažuriranja drugog parametra kod generiranja novog \(\sigma^2\) korišten je sljedeći identitet:
\[\sum_{i=1}^{n}\left(x_i-\mu\right)^2= (n-1)s^2_n +n \left(\bar{x}_n-\mu\right)^2.\]
Sljedeći dio koda grafički ilustrira iteracije u Gibbsovom uzorkovanju:
Kod - iteracije Gibbsovog uzorkovanja
par(mfrow=c(1,3),mar=c(2.75,2.75,.5,.5),mgp=c(1.70,.70,0))
m1<-5
plot( PHI[1:m1,],type="l",xlim=range(PHI[1:100,1]), ylim=range(PHI[1:100,2]),
lty=1,col="gray",xlab=expression(theta),ylab=expression(tilde(sigma)^2))
text( PHI[1:m1,1], PHI[1:m1,2], c(1:m1) )
m1<-15
plot( PHI[1:m1,],type="l",xlim=range(PHI[1:100,1]), ylim=range(PHI[1:100,2]),
lty=1,col="gray",xlab=expression(theta),ylab=expression(tilde(sigma)^2))
text( PHI[1:m1,1], PHI[1:m1,2], c(1:m1) )
m1<-100
plot( PHI[1:m1,],type="l",xlim=range(PHI[1:100,1]), ylim=range(PHI[1:100,2]),
lty=1,col="gray",xlab=expression(theta),ylab=expression(tilde(sigma)^2))
text( PHI[1:m1,1], PHI[1:m1,2], c(1:m1) )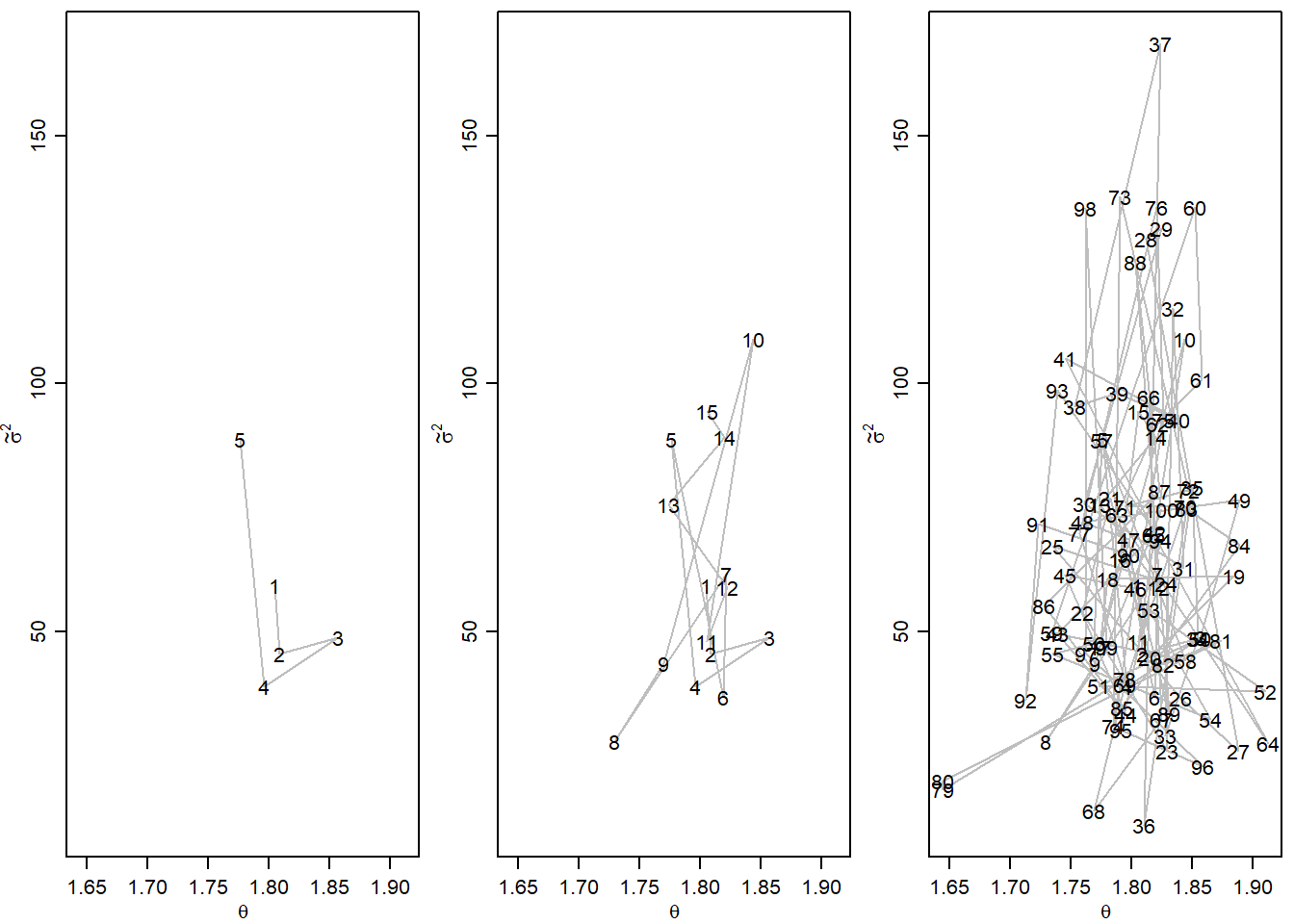
Na sljedećim prikazima možemo vidjeti uzorak generiran Gibssovim uzorkovanjem, empirijske marginalne distribucije s vertikalniim linijama koje reprezentiraju pouzdani interval tako dobivene empirijske distribucije i rezultata koji bi dao frekvencionistički pouzdani interval za očekivanje.
Kod - uzorak dobiven Gibbsovim uzorkovanjem
# grid
G<-100 ; H<-100
mean.grid<-seq(1.505,2.00,length=G)
prec.grid<-seq(1.75,175,length=H)
post.grid<-matrix(nrow=G,ncol=H)
for(g in 1:G) {
for(h in 1:H) {
post.grid[g,h]<- dnorm(mean.grid[g], mu0, sqrt(t20)) *
dgamma(prec.grid[h], nu0/2, s20*nu0/2 ) *
prod( dnorm(y,mean.grid[g],1/sqrt(prec.grid[h])) )
}
}
post.grid<-post.grid/sum(post.grid)
par(mfrow=c(1,3),mar=c(2.75,2.75,.5,.5),mgp=c(1.70,.70,0))
sseq<-1:1000
image( mean.grid,prec.grid,post.grid,col=gray( (10:0)/10 ),
xlab=expression(theta), ylab=expression(tilde(sigma)^2) ,
xlim=range(PHI[,1]),ylim=range(PHI[,2]) )
points(PHI[sseq,1],PHI[sseq,2],pch=".",cex=1.25 )
plot(density(PHI[,1],adj=2), xlab=expression(theta),main="",
xlim=c(1.55,2.05),
ylab=expression( paste(italic("p("),
theta,"|",italic(y[1]),"...",italic(y[n]),")",sep="")))
abline(v=quantile(PHI[,1],prob=c(.025,.975)),lwd=2,col="gray")
n<-length(y) ; ybar<-mean(y) ; s2<-var(y);
abline( v= ybar+qt( c(.025,.975), n-1) *sqrt(s2/n), col="black",lwd=1)
plot(density(PHI[,2],adj=2), xlab=expression(tilde(sigma)^2),main="",
ylab=expression( paste(italic("p("),
tilde(sigma)^2,"|",italic(y[1]),"...",italic(y[n]),")",sep=""))) 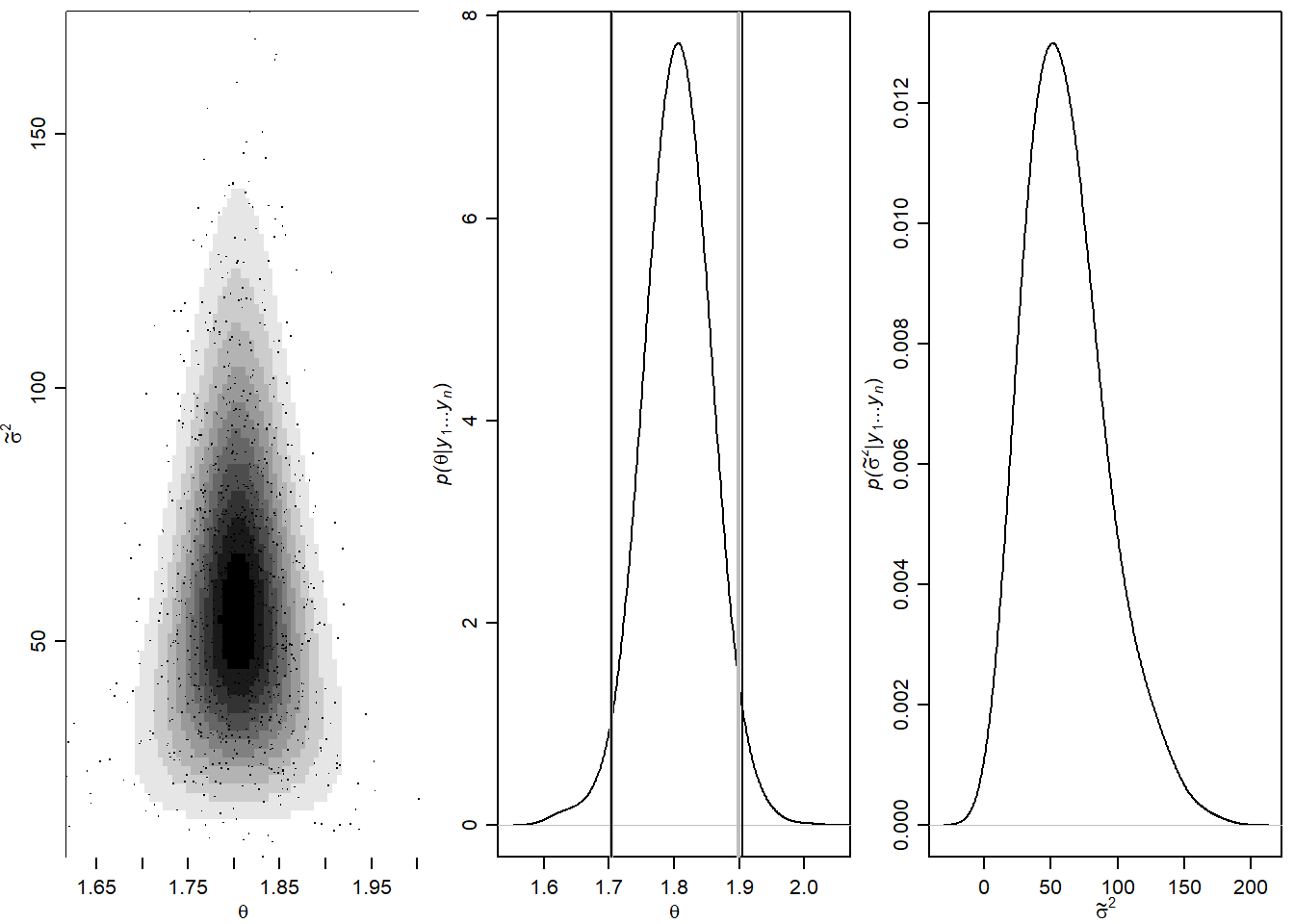
Efektivne veličine uzoraka i pripadne autokorelacije na koraku 1: \[S_{eff}(\theta)=1152, \quad S_{eff}(\sigma^2)=1166, \quad acf_{\theta}(1)=0.044, \quad acf_{\sigma^2}(1)=0.096\]
effectiveSize(PHI[,1]) var1
1151.948 acf(PHI[,1])[1]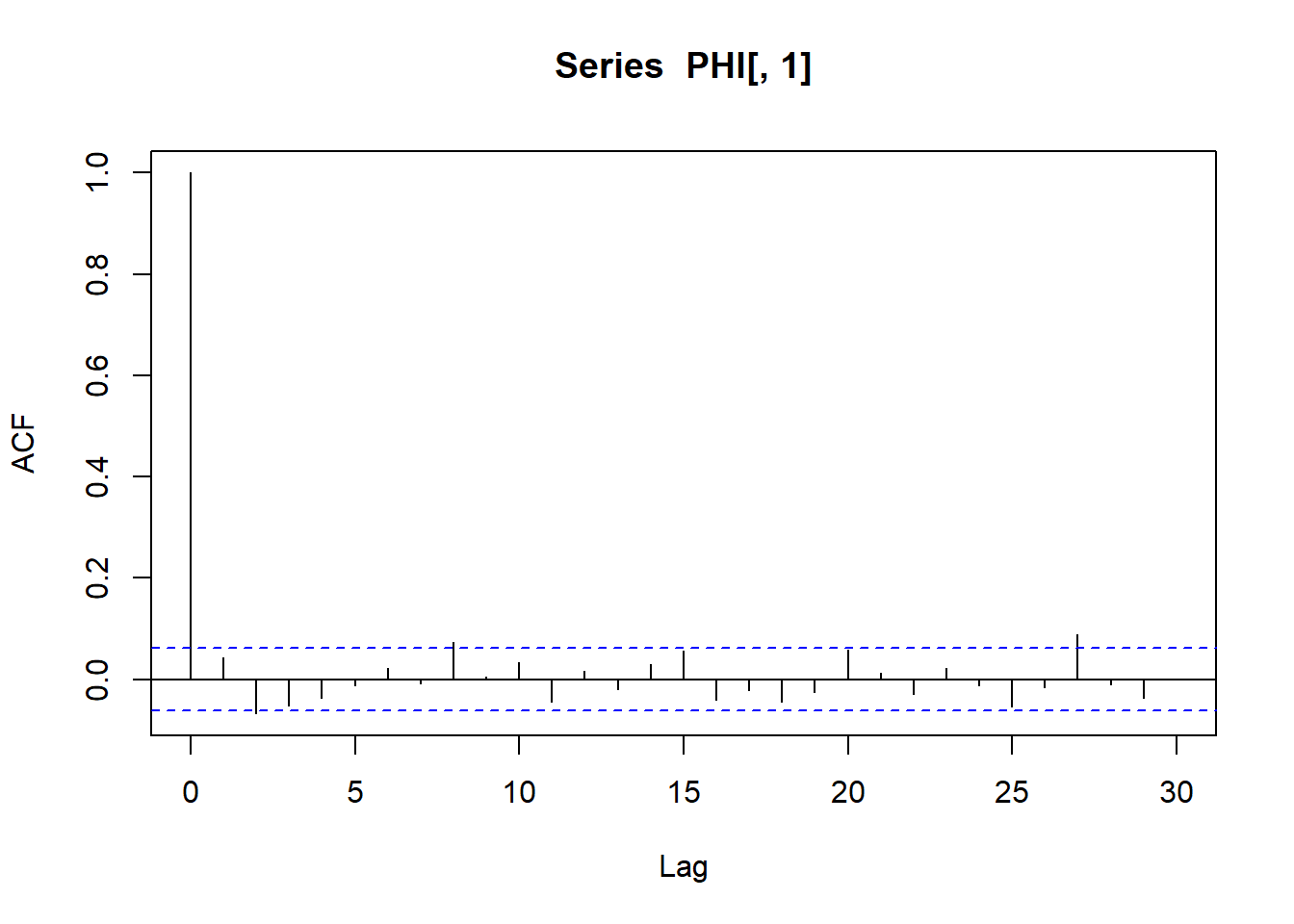
Autocorrelations of series 'PHI[, 1]', by lag
1
0.044 effectiveSize(PHI[,2]) var1
1166.018 acf(PHI[,2])[1]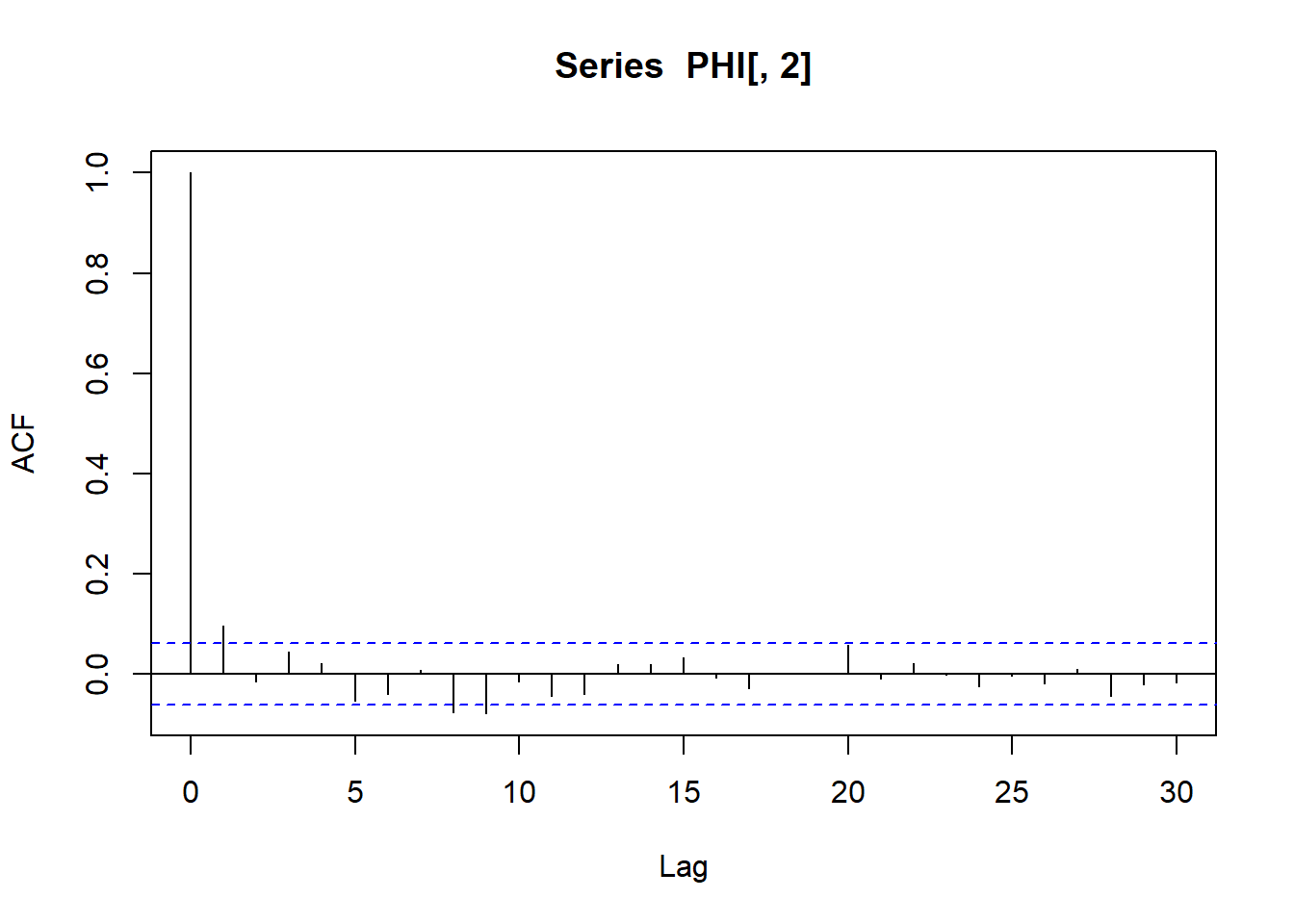
Autocorrelations of series 'PHI[, 2]', by lag
1
0.096 Dobivene mjere sugeriraju da je MCMC lanac konvergirao i da je aproksimacija približno kvalitetna kao MC aproksimacija dimnezije $ 1200$. Autokorelacija na lagu 1 je vrlo mala.
5.2.3 O brzini konvergencije MCMC metoda
Za MCMC aproksimaciju integrala \(\int_A f(\phi)d\phi\), gdje je \(f\) neka gustoća, od presudne važnosti je da Markovljev lanac provede vrijeme u skupu \(A\) proporcionalno sa stvarnom vjerojatnošću \(P(A)=\int_A f(\phi)d\phi\).
U svrhu ilustracije, neka su \(A_1\), \(A_2\) i \(A_3\) skupovi takvi da je \(P(A_2) < P(A_1) \approx P(A_3)\). Da bi MCMC aproksimacija bila dobra ML bi trebao najmanje vremena provesti u skupu \(A_2\), a podjednako (više) vremena u \(A_1\) i \(A_3\). Općenito, ukoliko ML kreće iz stanja koje se nalazi u području male vjerojatnosti, trebat će nam velik broj iteracija MCMC algoritma (\(S\)) dok ML
- ne izađe iz \(A_2\) i prijeđe u područje veće vjerojatnosti i
- ne prošeće između \(A_1\) i \(A_3\) kao i ostalih skupova velike vjerojatnosti.
Pri tome, 1) dovodimo u vezu sa stacionarnošću, odnosno konvergencijom lanca (ukoliko ML kreće iz područja s velikom vjerojatnošću stacionarnost nije problem ).
S druge strane 2) dovodimo u vezu s brzinom kretanja ML kroz parametarski prostor koje se formalno zove “brzina miješanja” (eng. speed of mixing). MC metode imaju savršenu brzinu miješanja (mixing) jer nezavisno uzorkujemo (nema korelacije). S druge strane, MCMC metode imaju lošu brzinu miješanja zbog koreliransti u uzorku.
Postavlja se pitanje koliko koreliranost utječe na brzinu miješanja/kvalitetu aproksimacije? Ilustrirajmo to na primjeru aproksimacije očekivanja \(E[\phi]=\phi_0=\int \phi f(\phi) d\phi\). Pretpostavimo da raspolažemo slučajnim uzorkom \((\phi^{(1)}, \dots, \phi^{(S)})\). Nepristran (frekvencionistički) procjenitelj za \(\phi_0\) je \(\bar{\phi}=\frac{1}{S}\sum_{s=1}^{S}\phi^{(s)}\).
- MC metoda (nezavisno uzorkovanje)
\[Var_{MC}\left[\bar{\phi}\right]=E\left[\left(\bar{\phi}-\phi_0\right)^2\right]=\frac{Var \phi}{S}, \quad Var\phi=\int \left(\phi - \phi_0\right)^2 f(\phi) d\phi.\] Pri tome je \(\sqrt{Var_{MC}\left[\bar{\phi}\right]}\) pripadna Monte Carlo standardna greška (govori nam koliko dobro očekujemo da \(\bar{\phi}\) aproksimira \(\phi_0\)). Drugim riječima (prema CGT), interval \[\left[\bar{\phi}-2\sqrt{Var_{MC}(\bar{\phi})}, \bar{\phi}+2\sqrt{Var_{MC}(\bar{\phi})}\right]\] bi u pravilu u približno \(95\%\) slučajeva sadržavao stvarnu vrijednost \(\phi_0\).
- MCMC metoda (npr. Metropolis-Hastings algoritam, Gibbsovo uzorkovanje)
\[\begin{align*} Var_{MC}\left[\bar{\phi}\right]&=E\left[\left(\bar{\phi}-\phi_0\right)^2\right]=E\left[\left(\frac{1}{S}\sum_{s=1}^{S} \left(\phi^{(s)}-\phi_0\right)\right)^2\right] \\ &= \frac{1}{S^2}\sum_{s=1}^{S}E\left[\left(\phi^{(s)}-\phi_0 \right)^2\right]+\frac{1}{S^2}\sum_{s\neq t}E\left[\left(\phi^{(s)}-\phi_0\right)\left(\phi^{(t)}-\phi_0\right)\right] \\ &= Var_{MC}\left[\bar{\phi}\right]+\frac{1}{S^2}\sum_{s\neq t}E\left[\left(\phi^{(s)}-\phi_0\right)\left(\phi^{(t)}-\phi_0\right)\right] \end{align*}\], pri čemu zadnji član ovisi o korelaciji u ML i uvijek je pozitivan.
U tom kontekstu uočavamo \[Var_{MCMC}\left[\bar{\phi}\right] >Var_{MC}\left[\bar{\phi}\right]. \] Riječima, MCMC aproksimacija je uvijek lošija od MC aproksimacije, a što je autokorelacija u lancu veća to je aproksimacija lošija.
Korisna usporedba MC i MCMC metoda radimo s tzv. efektivnom veličinom uzorka (eng. effective sample size):
Broj \(S_{eff}\) t.d. je \(Var_{MCMC}\left[\bar{\phi}\right]=Var\left[\phi\right]/S_{eff}\) nazivamo efektivna veličina uzorka.
Interpretiramo ga kao broj nezavisnih generiranja MC metode potreban da dobijemo istu preciznost kao MCMC metoda koju koristimo.
Generalno, MC metoda oslanjanju se na jaki zakon velikih brojeva kako bi opravdali korištenje empirijske distribucije simuliranih vrijednosti u svrhu aproksimacije posteriorne distribucije.
S druge strane, MCMC metode oslanjanju se na ergodski teorem za Markovljeve lance (svojevrsna generalizacija JZVB u kontekstu ML) koji osigurava:
- \[P(\phi^{(s)} \in A) \to \int_A f(\phi | \mathbb{x}) d\phi, \quad S \to \infty\]
- \[\frac{1}{S}\sum_{s=1}^{S} g(\phi^{(s)}) \to E\left[g(\phi) | \mathbb{X}=\mathbb{x}\right]=\int g(\phi) f(\phi | \mathbb{x}) d\phi, \quad S \to \infty.\]
Zbog strukture zavisnosti niza generiranih vrijednosti \((\phi^{(1)}, \dots, \phi^{(S)})\) kao Markovljevog lanca, postoji snažna koreliranost među vrijednostima niza, pa (nerijetko) trebamo simulirati daleko više vrijednosti nego u slučajnu MC metoda kako bi osigurali zadovoljavajuće aproksimacije.
Zbog toga je uvijek dobro provjeriti kakva je koreliranost lanca korištene MCMC metode pomoću
acf()na različitim koracima (“lagovima”), npr. 1, 10, 50.
5.2.4 (Ostale) MCMC metode i njihova implementacija
U prethodnim poglavljima detaljnije smo objasnili Metropolis-Hastings algoritam i Gibbsovo uzorkovanje. Intuitivno je jasno da u jednodimenzionalnim parametarskim modelima koristimo Metropolis-Hasintgs algoritam, dok u multivarijatnom slučaju koristimo Gibbsovo uzorkovanje. Samostalna (“ručna”) implementacija ovih algoritama postaje redudantna s povećanjem kompleksnosti Bayesovskog modela. Iz tog razloga nastale su mnoge implementacije ovih (i drugih) MCMC algoritama u svrhu aproksimacije posteriorne distribucije kao što su:
JAGS (“Just another Gibbs samples”): kao što i sam naziv kaže, radi se o implementaciji Gibbsovog uzorkovanja koja za nas obavlja tehnički posao, a mi trebamo samo unijeti komponente Bayesovskog modela (https://mcmc-jags.sourceforge.io/)
BUGS (“Bayesian inference Using Gibbs Sampling”): iako ne u potpunosti ista implementacija, radi slično što i JAGS (http://www.bayesianscientific.org/resource/bugs-openbugs-winbugs/)
STAN: radi se o implementaciji više vrsta MCMC metoda, a koje nisu Gibbsovo uzorkovanje, primjerice trenutno vrlo popularnoj Hamiltonian Monte Carlo (HMC) metodi (https://mc-stan.org/)
install.packages("rstan", repos = c("https://mc-stan.org/r-packages/", getOption("repos")))
library("rstan")
options(mc.cores = parallel::detectCores())
rstan_options(auto_write = TRUE)STAN struktura u R-u tipično izgleda ovako:
MojeImeModela <- " #Ime modela
data {
real <lower = _, upper = _> x[broj_podataka]; // podaci
}
parameters {
real parametar1; //realni parametar
real<lower = 0> parametar2;
}
model {
x ~ ime_distribucije(parametri_distribucije); // vjerodostojnost
parametar1 ~ ime_distribucije(hiperparametri) //apriorne distribucije (ukoliko nisu definirane, default su slabo informativne apriorne distribucije)
parametar2 ~ ime_distribucije(hiperparametri)
}
generated quantities { //funkcije parametra koje želimo generirati (primjerice prediktivne vrijednosti)
real x_tilda = imedistribucije_rng(parametri);
}"
simulacija<-stan(
model_code = ______, #IMe modela
data = list(x=_____), # Podaci
chains = ______, # broj korištenih Markovljevih lanaca
warmup = _____, # burn in period za svaki lanac
iter = _____, # ukupan broj iteracija svakog lanca
cores = _____, # broj korištenih jezgri
refresh = _____, # no progress show
seed=____
)Nakon generiranja simuliranih vrijednosti posteriorne distribucije, analizu brzine konvergencije i brzine miješanja algoritma, kao i vizualni/sumarni pregled posteriorne distribucije dobivamo na sljedeći način:
# grafički prikaz gustoće/histograma za pojedinihi parametar koristeći sve lanace algoritma zajednp
# pars je ime parametra za kojeg crtamo usporedbu
mcmc_dens(my_sim, pars = "___") +
yaxis_text(TRUE) +
ylab("density")
mcmc_hist(my_sim, pars = "___") +
yaxis_text(TRUE) +
ylab("count")
# Vizualna dijagnostika: trajektorija simuliranih vrijednosti parametara
mcmc_trace(my_sim, pars = "___", size = 0.5)
mcmc_trace(my_sim, pars = "___", size = 0.5, window = c(0, ___)) # Zumirani prikaz
# Vizualna dijagnostika: prikaz gustoće za pojedini parametar za svaki lanac posebno - služi za usporedbu je li došlo do konvergencije
mcmc_dens_overlay(my_sim, pars = "___")
# Vizualna dijagnostika: autokorelacijska funkcija za pojedini parametar - govori o brzini miješanja lanca
mcmc_acf(my_sim, pars = "___")
# Numerička dijagnostika: Rhat,efektivna veličina uzorka, sumarni pregled numeričkih karakteristika posteriorne distribucije pojedinog parametra
print(MojeImeModela)
#dohvacanje simuliranih vrijednosti
#parametra
rstan::extract(sim.MCMC.stan, permuted = TRUE) Koju od implementacija izabrati za korištenje nije jednostavno odgovoriti i ovisi o više faktora, posebice o vrsti problema koji proučavamo. Primjerice, u slučaju (semi)-konjugatnih Bayesovskih modela obično JAGS-ova implementacija Gibbsovog uzorkovanja funkcionira jako dobro, dok u općenitijem i kompleksnijem slučaju HMC metode implementirane u platformi STAN daju bolje rezultate.
5.3 Zadaci
Zadatak 5.1 Za zadatak 3.4 na temelju zadane vjerodostojnosti i apriorne distribucije odredite:
- Monte Carlo aproksimaciju pripadnih posteriornih distribucija uz grafičku vizualizaciju konvergencije aproksimacije.
- Monte Carlo aproksimaciju posteriornog očekivanja uz grafičku vizualizaciju konvergencije aproksimacije.
- Odredite Monte Carlo aproksimaciju posteriorne vjerojatnosti da je stopa pojavljivanja potresa barem 2 po satu uz usporedbu sa stvarnom vjerojatnosti.
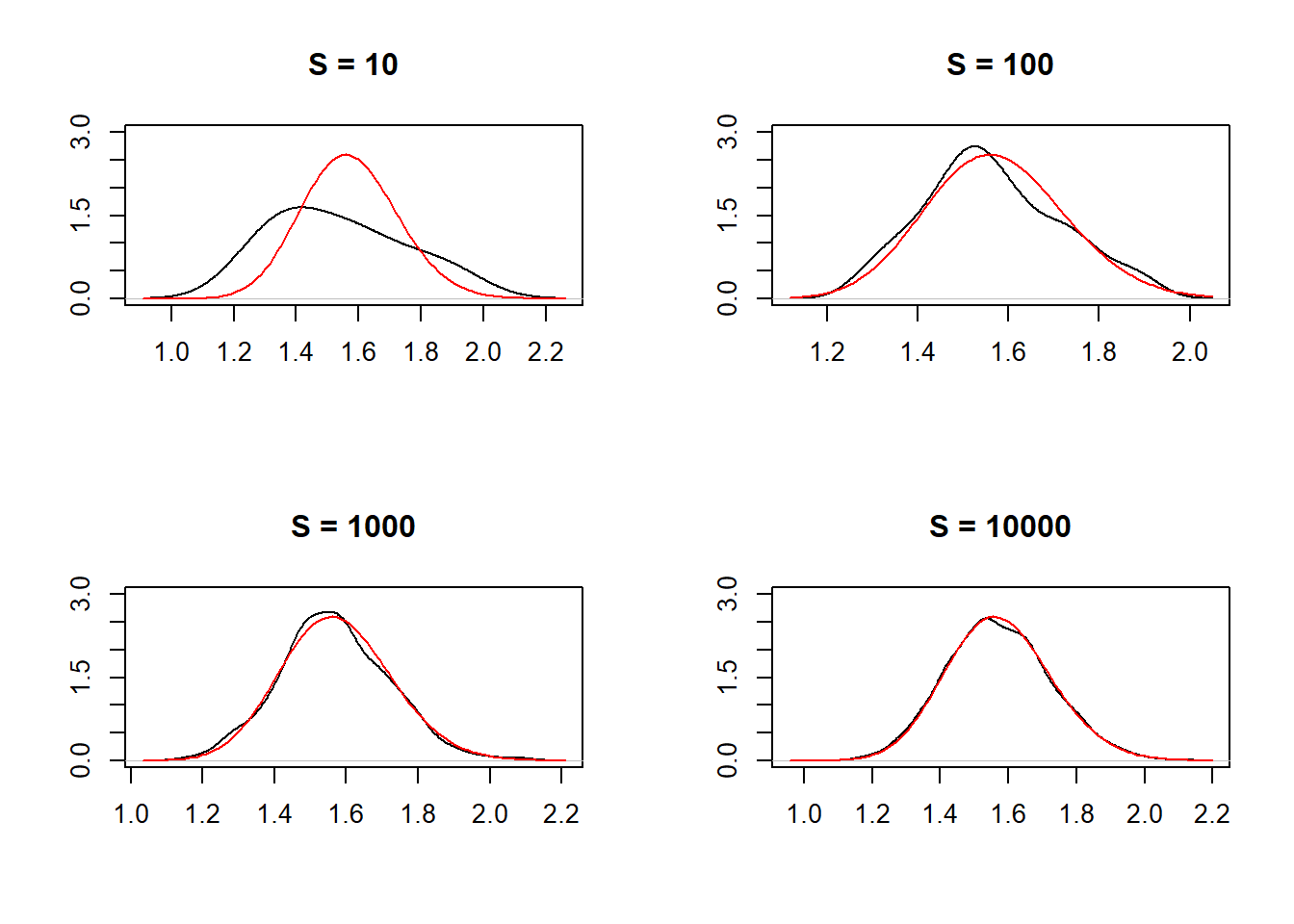
- Vizualizacija konvergencije Monte Carlo aproksimacije posteriorne distribucije \(f(\lambda | x_1, \dots, x_n)\) prema stvarnoj distribuciji (crvena boja).
alpha <- 4
beta <- 3
sum.x<- 63.09
n<-100
par(mfrow=c(2,2))
for(i in c(10,100,1000,10000))
{
lambda.mc <- rgamma(i,alpha+n,beta+sum.x)
plot(density(rgamma(i,104,66.09)),ylim = c(0, 3), main = paste("S =",i), xlab="", ylab="")
curve(dgamma(x, alpha+n,beta+sum.x), col = 'red', add=T)
}
- Monte Carlo aproksimacija posteriornog očekivanja:
aprox.po<-c()
for(i in c(10,100,1000,10000))
{
lambda.mc <- rgamma(i,alpha+n,beta+sum.x)
aprox.po<-c(aprox.po,mean(lambda.mc))
}
aprox.po[1] 1.558213 1.583106 1.565242 1.573105Prema tome Monte Carlo aproksimacija posteriornog očekivanja dimenzije \(S=10000\) je \[ \frac{1}{10000}\sum_{s=1}^{10000}\lambda^{(10000)}=1.573105 \] dok je stvarna vrijednost posteriornog očekivanja \[E[\lambda | X_1=x_1, \dots, X_n=x_n]=1.573612.\]
(alpha+n)/(beta+sum.x)[1] 1.573612- Monte Carlo aproksimacija posteriorne vjerojatnosti \(P(\lambda >2 | X_1=x_1, \dots, X_n=x_n)\):
aprox.pv2<-c()
for(i in c(10,100,1000,10000,100000,1000000))
{
lambda.mc <- rgamma(i,alpha+n,beta+sum.x)
aprox.pv2<-c(aprox.pv2,mean(lambda.mc>2))
}
aprox.pv2[1] 0.000000 0.020000 0.007000 0.005700 0.005110 0.005003Stoga je tražena aproksimacija \[\frac{1}{10000}\sum_{s=1}^{10000} I_{\{\lambda^{(s)} > 2\}}=0.005003\] dok je stvarna vrijednost \[P(\lambda >2 | X_1=x_1, \dots, X_n=x_n)=0.00495458.\]
Zadatak 5.2 Riješite zadatke 3.4 - 3.7 koristeći Monte Carlo aproksimacije uz prikladne usporedbe sa stvarnim vrijednostima.
Zadatak 5.3 U bazi podataka midge (iz paketa Flury) nalaze se podaci o duljini krila dviju vrsta mušica (Amerohelea fasciata (Af) i Pseudofasciata (Apf)). Pretpostavka je da mjerenja dolaze iz normalne distribucije. Prethodna istraživanja sugeriraju da je očekivana duljina krila za mušice \(1.9 mm\) uz standardnu devijaciju \(0.1\).
- Koji su parametri od interesa? Zapišite vjerodostojnost Bayesovog modela za pojedinu vrstu
- Odredite konjugiranu apriornu distribuciju i pripadnu posteriornu distribuciju za pojedine vrste.
- Aproksimirajte posteriornu očekivanu vrijednost duljine krila mušice za pojedinu vrstu korištenjem Monte Carlo aproksimacija.
- Nakon što uzmemo podatke u obzir, koliko iznosi aproksimacija vjerojatnosti da je očekivana duljina krila pojedine vrste mušice veća od 2 mm?
- Odredite posteriorne \(0.05\)-vjerodostojne intervale za očekivanja pojedinih vrsta
install.packages("remotes")
library(remotes)
install_version("Flury", "0.1-3")
library(Flury)- \(\left(\mu_1, \sigma^2_1 \right) \in \mathbb{R} \times \langle 0, +\infty\rangle\), gdje su \(\mu_1\) i \(\sigma^2_1\) redom očekivana duljina i varijanca krila mušice vrste Af
- \(\left(\mu_2, \sigma^2_2 \right) \in \mathbb{R} \times \langle 0, +\infty\rangle\), gdje su \(\mu_2\) i \(\sigma^2_2\) redom očekivana duljina i varijanca krila mušice vrste Af
Pripadne vjerodostojnosti: \[f(x | \mu_1, \sigma^2_1)=\frac{1}{\sqrt{2\pi \cdot \sigma^2_1}}e^{-\frac{\left(x-\mu_1\right)^2}{2\cdot \sigma^2_1}}, \quad f(y | \mu_2, \sigma^2_2)=\frac{1}{\sqrt{2\pi \cdot \sigma^2_2}}e^{-\frac{\left(y-\mu_2\right)^2}{2\cdot \sigma^2_2}}.\] b) Radi se o normalnom modelu uz oba parametra nepoznata.
Apriorne distribucije: S obzirom da nemamo nikakve dodatne informacije o (novim) vrstama mušica, za apriorne parametre koristimo zajedničke vrijednosti \[\nu_0=1, k_0=1, \,\mu_0=1.9, \, \sigma^2_0=0.01\] Pri tome treba napomenuti da \(\mu_0\) i \(\sigma^2_0\) reflektiraju informacije o prijašnjim istraživanjima za mušice općenito, a kako se radi o novim mušicama, postavljamo apriorne dimenzije “uzoraka” \(\nu_0=k_0=1\).
Stoga je:
- \(\sigma^2_1 \sim InvGama(\frac{1}{2}, \frac{1}{2}\cdot 0.01), \quad \mu_1 |\sigma^2_1 \sim \mathcal{N}(1.9, \frac{\sigma^2_1}{1})\)
- \(\sigma^2_2 \sim InvGama(\frac{1}{2}, \frac{1}{2}\cdot 0.01), \quad \mu_2 |\sigma^2_2 \sim \mathcal{N}(1.9, \frac{\sigma^2_2}{1}).\)
Posteriorne distribucije: Znamo da je uz zadane konjugirane apriorne distribucije, posteriorna distribucija oblika:
- \(\sigma^2_1 \sim InvGama(\frac{\nu_9}{2}, \frac{\nu_9}{2}\cdot \sigma^2_9), \quad \mu_1 |\sigma^2_1 \sim \mathcal{N}(\mu_9, \frac{\sigma^2_9}{\nu_9})\)
- \(\sigma^2_2 \sim InvGama(\frac{\nu_6}{2}, \frac{\nu_6}{2}\cdot \sigma^2_6), \quad \mu_2 |\sigma^2_2 \sim \mathcal{N}(\mu_6, \frac{\sigma^2_6}{\nu_6}),\)
gdje su
- \(\nu_9=10, \, k_9=10, \, \mu_9=1.814,\, \sigma^2_9=\frac{1}{10}\left(1\cdot 0.01+(9-1) s^2_9+\frac{1\cdot 9}{10}\left(\bar{x}_9-1.9\right)^2\right)=0.006\)
- \(\nu_6=7, \, k_6=7, \, \mu_6=1.923,\, \sigma^2_6=\frac{1}{7}\left(1\cdot 0.01+(6-1) s^2_6+\frac{1\cdot 6}{7}\left(\bar{y}_6-1.9\right)^2\right)=0.01\)
data(midge)
attach(midge)
# vrsta Af
nu0.Af <- 1
k0.Af <- 1
mu0.Af <-1.9
sigma0.Af <-0.1
bar.Af <-mean(Wing.Length[Species=="Af"])
n.Af <- length(Wing.Length[Species=="Af"])
s2.Af <-var(Wing.Length[Species=="Af"])
kn.Af<- k0.Af+n.Af
nun.Af<-nu0.Af+n.Af
mun.Af <-(k0.Af*mu0.Af+n.Af*bar.Af)/kn.Af
sigman.Af <- sqrt((nu0.Af*sigma0.Af^2+(n.Af-1)*s2.Af+k0.Af*n.Af*(bar.Af-mu0.Af)/kn.Af)/nun.Af)
mun.Af[1] 1.814sigman.Af^2[1] 0.005902222# vrsta Apf
nu0.Apf <- 1
k0.Apf <- 1
mu0.Apf <-1.9
sigma0.Apf <-0.1
bar.Apf <-mean(Wing.Length[Species=="Apf"])
n.Apf <- length(Wing.Length[Species=="Apf"])
s2.Apf <-var(Wing.Length[Species=="Apf"])
kn.Apf<- k0.Apf+n.Apf
nun.Apf<-nu0.Apf+n.Apf
mun.Apf <-(k0.Apf*mu0.Apf+n.Apf*bar.Apf)/kn.Apf
sigman.Apf <- sqrt((nu0.Apf*sigma0.Apf^2+(n.Apf-1)*s2.Apf+k0.Apf*n.Apf*(bar.Apf-mu0.Apf)/kn.Apf)/nun.Apf)
mun.Apf[1] 1.922857sigman.Apf^2[1] 0.01025578- Primijetimo da nas zanima Monte Carlo aproksimacija \(E[\mu_1 | X_1=x_1, \cdots, X_9=x_9]\) i \(E[\mu_2 | Y_1=y_1, \cdots, Y_6=x_6]\).
#vrsta Af
sigma2.mc.Af <- 1/rgamma(10000, nun.Af, nun.Af*sigman.Af^2/2)
mu.mc.Af <- rnorm(10000, mun.Af, sqrt(sigma2.mc.Af/kn.Af))
mean(mu.mc.Af)[1] 1.81379#vrsta Apf
sigma2.mc.Apf <- 1/rgamma(10000, nun.Apf, nun.Apf*sigman.Apf^2/2)
mu.mc.Apf <- rnorm(10000, mun.Apf, sqrt(sigma2.mc.Apf/kn.Apf))
mean(mu.mc.Apf)[1] 1.922698Dakle, Monte Carlo aproksimacije očekivanih duljina krila su:
\[E[\mu_1 | X_1=x_1, \cdots, X_9=x_9]\approx 1.814, \quad E[\mu_2 | Y_1=y_1, \cdots, Y_6=x_6] \approx 1.923\]
S druge strane, Monte Carlo aproksimacije vjerojatnosti \(P(\mu_1 >2 | \{\mathbb{X}=\mathbb{x}\})\) i \(P(\mu_2 >2 | \{\mathbb{Y}=\mathbb{y}\})\) lako izračunamo sljedećim kodom:
mean(mu.mc.Af >2)[1] 0mean(mu.mc.Apf >2)[1] 0.008quantile(mu.mc.Af, c(0.025, 0.975)) 2.5% 97.5%
1.778559 1.849136 quantile(mu.mc.Apf, c(0.025, 0.975)) 2.5% 97.5%
1.865124 1.981767 Zaključujemo:
\[P(\mu_1 \in \langle 1.78, 1.85 \rangle | X_1=x_1, \dots, X_9=x_9) \approx 0.95 \] \[P(\mu_2 \in \langle 1.863 1.981 \rangle | Y_1=x_1, \dots, Y_6=y_6) \approx 0.95 \]
Zadatak 5.4 Zadan je gama-eksponencijalni model uz hiperparametre \(\alpha=1, \beta=2\) i podatke \(\mathbb{x}=(0.7, 1.2, 1.05, 0.9, 0.8, 1.1)\).
- Napravite MCMC aproksimaciju posteriorne distribucije parametra modela i grafički usporedite sa stvarnom distribucijom.
- Napravite MCMC aproksimaciju posteriorne prediktivne distribucije modela i grafički usporedite sa stvarnom distribucijom.
- Kako se radi o jednodimenzionalnom parametru provest ćemo Metropolis-Hastings algoritam za generiranje vrijednosti iz posteriorne distribucije uz simetričnu distribuciju kandidata (specijalno, radi se o Metropolis algoritmu).
S <- 20000
x <- c(0.7, 1.2, 1.05, 0.9, 0.8, 1.1)
alpha<-1
beta<-2
alphan <- alpha+length(x)
betan <-beta+sum(x)
delta <-0.2
lambda <- 0.9
lambda.MCMC <- NULL
for(s in 1:S)
{lambda.star<-runif(1,lambda-delta, lambda+delta)
log.r <- (sum(dexp(x,lambda.star, log=TRUE))+dgamma(lambda.star,alpha, beta, log=TRUE))-
(sum(dexp(x,lambda, log=TRUE))+dgamma(lambda,alpha,beta, log=TRUE))
if (log(runif(1)) < log.r) {lambda <-lambda.star}
lambda.MCMC <-c(lambda.MCMC, lambda)
}
plot(density(lambda.MCMC), col="blue", xlab="Posteriorna distribucija")
curve(dgamma(x,alphan, betan), add=T, col="red")
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 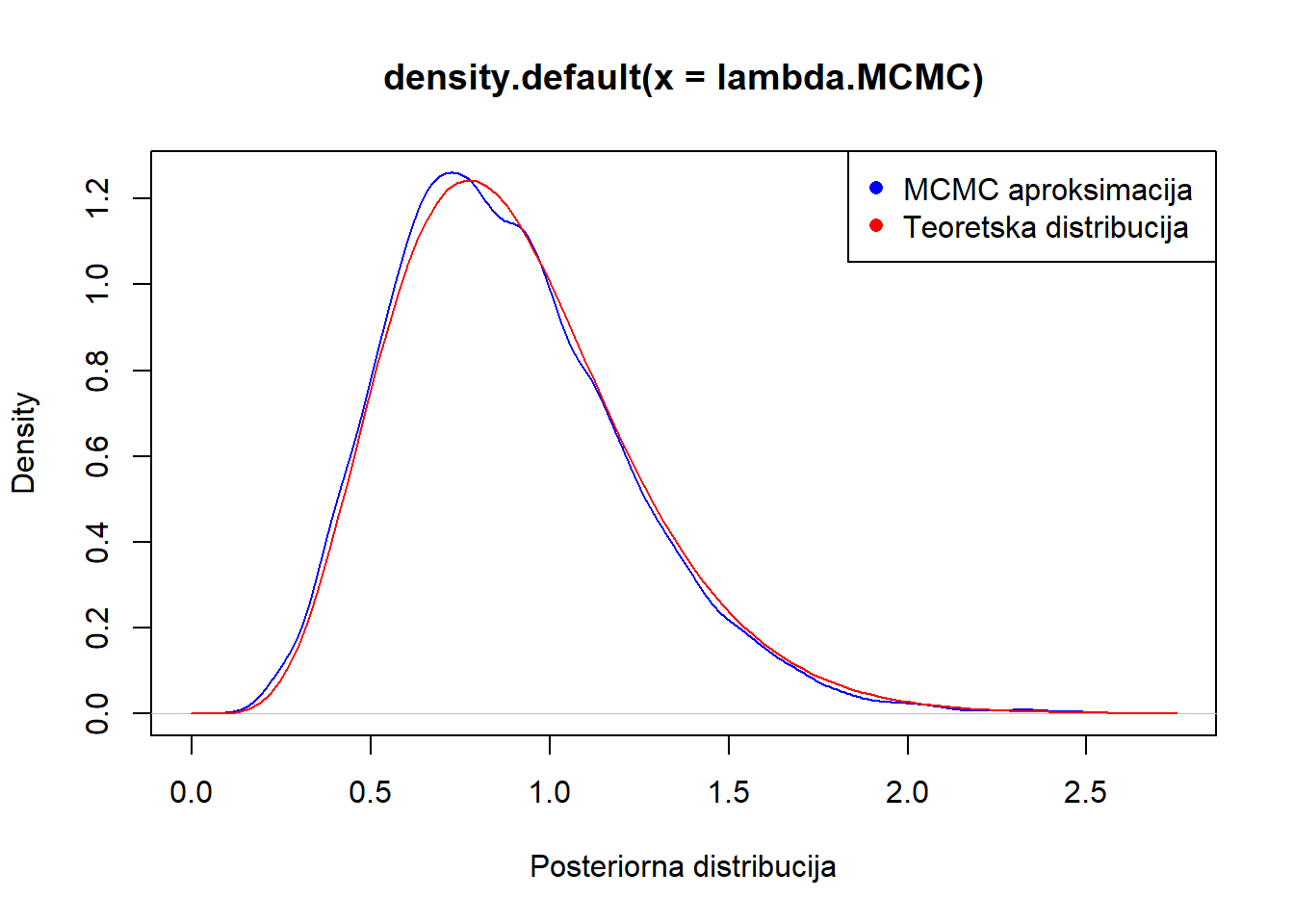
- Koristeći MCMC generirane vrijednosti za parametar \(\lambda\) možemo generirati nove “podatke”, odnosno predikcije iz vjerodostojnosti:
x.pred.MCMC <- rexp(S,lambda.MCMC)
plot(density(x.pred.MCMC), col="blue", xlab="Prediktivna posteriorna distribucija")
curve(dlomax(x,1/(betan),alphan), add=T, col="red")
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 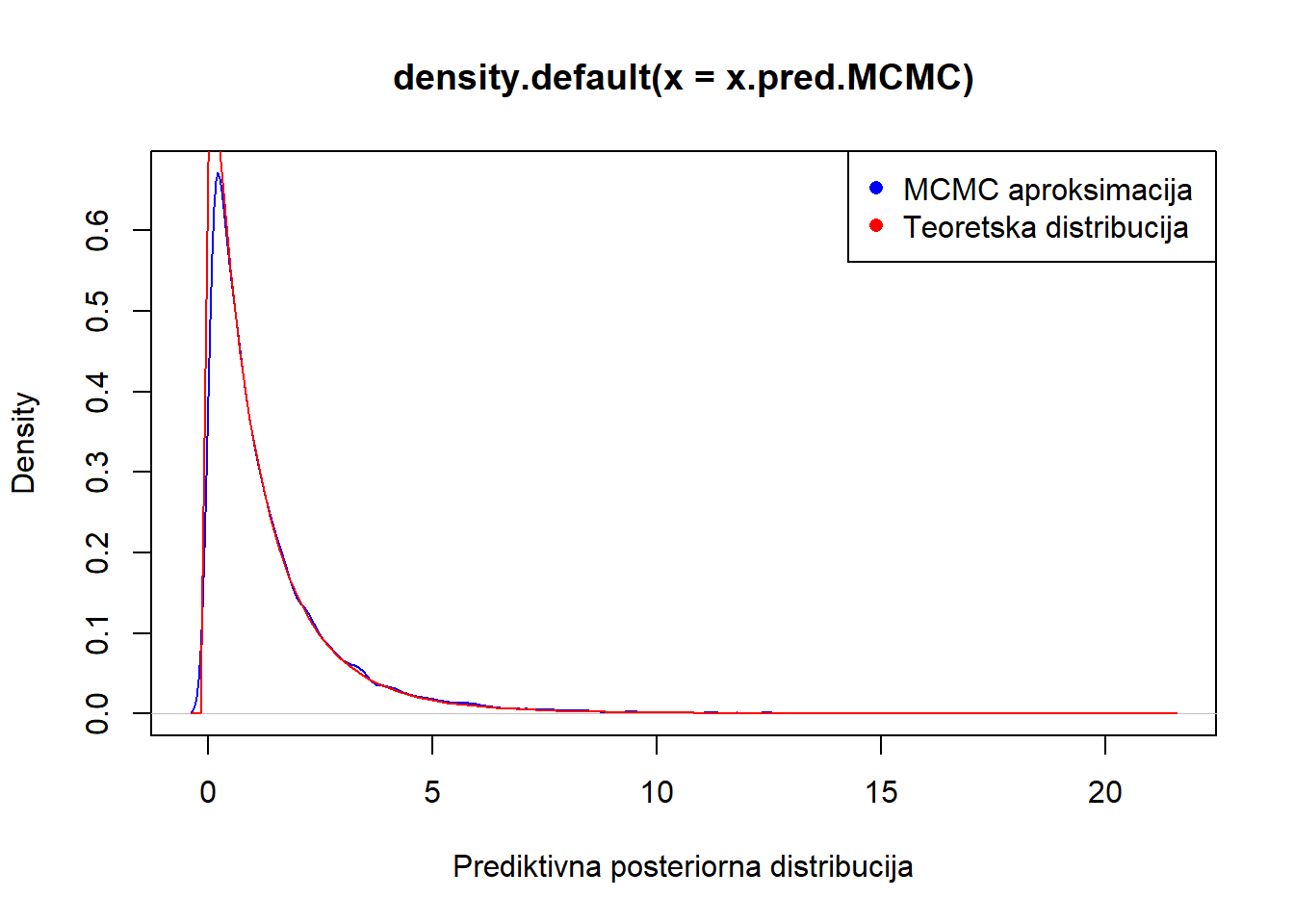
Zadatak 5.5 Zadan je beta-binomni model (broj izvođenja pokusa \(m=10\)) uz hiperparametre \(\alpha=2, \beta=2\) i podatke \(\mathbb{x}=(3,7,5,4,7,9,4,5,2)\).
- Napravite MCMC aproksimaciju posteriorne distribucije parametra modela i grafički usporedite sa stvarnom distribucijom.
- Napravite MCMC aproksimaciju posteriorne prediktivne distribucije modela i grafički usporedite sa stvarnom distribucijom.
- Napravite MCMC aproksimaciju posteriorne distribucije logaritma šansi parametra.
- Kako se radi o jednodimenzionalnom parametru provest ćemo Metropolis-Hastings algoritam za generiranje vrijednosti iz posteriorne distribucije uz simetričnu distribuciju kandidata (specijalno, radi se o Metropolis algoritmu).
S <- 20000
x <- c(3,7,5,4,7,9,4,5,2)
alpha<-2
beta<-2
m<-10
alphan <- alpha+sum(x)
betan <-beta+m*length(x)-sum(x)
delta <-0.05
theta <- 0.6
theta.MCMC <- NULL
for(s in 1:S)
{theta.star<-runif(1,theta-delta, theta+delta)
log.r <- (sum(dbinom(x,m,theta.star, log=TRUE))+dbeta(theta.star,alpha, beta, log=TRUE))-
(sum(dbinom(x,m,theta, log=TRUE))+dbeta(theta,alpha,beta, log=TRUE))
if (log(runif(1)) < log.r) {theta <-theta.star}
theta.MCMC <-c(theta.MCMC, theta)
}
plot(density(theta.MCMC), col="blue", xlab="Posteriorna distribucija")
curve(dbeta(x,alphan, betan), add=T, col="red")
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 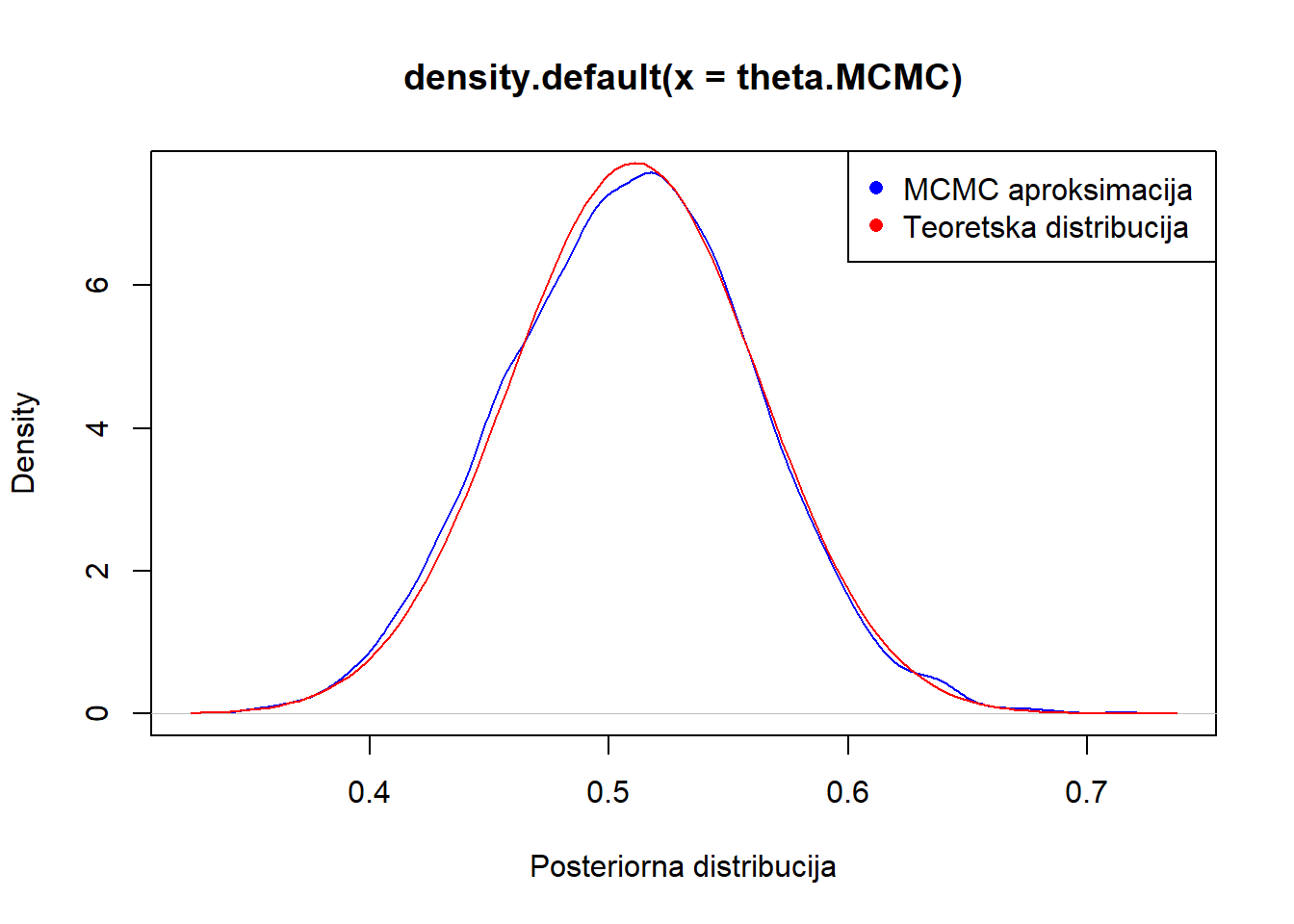
- Koristeći MCMC generirane vrijednosti za parametar \(\lambda\) možemo generirati nove “podatke”, odnosno predikcije iz vjerodostojnosti:
x.pred.MCMC <- rbinom(S,m,theta.MCMC)
plot(prop.table(table(x.pred.MCMC)), col="blue", xlab="Prediktivna posteriorna distribucija")
points(c(0:10)-0.1, dbbinom(c(0:10), m,alphan,betan), col="red" ,type="h",
ylab=expression(paste(italic("p("),y[n+1],"|",y[1],"...",y[n],")",sep="")),
xlab=expression(italic(y[n+1])),ylim=c(0,.5),lwd=3)
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 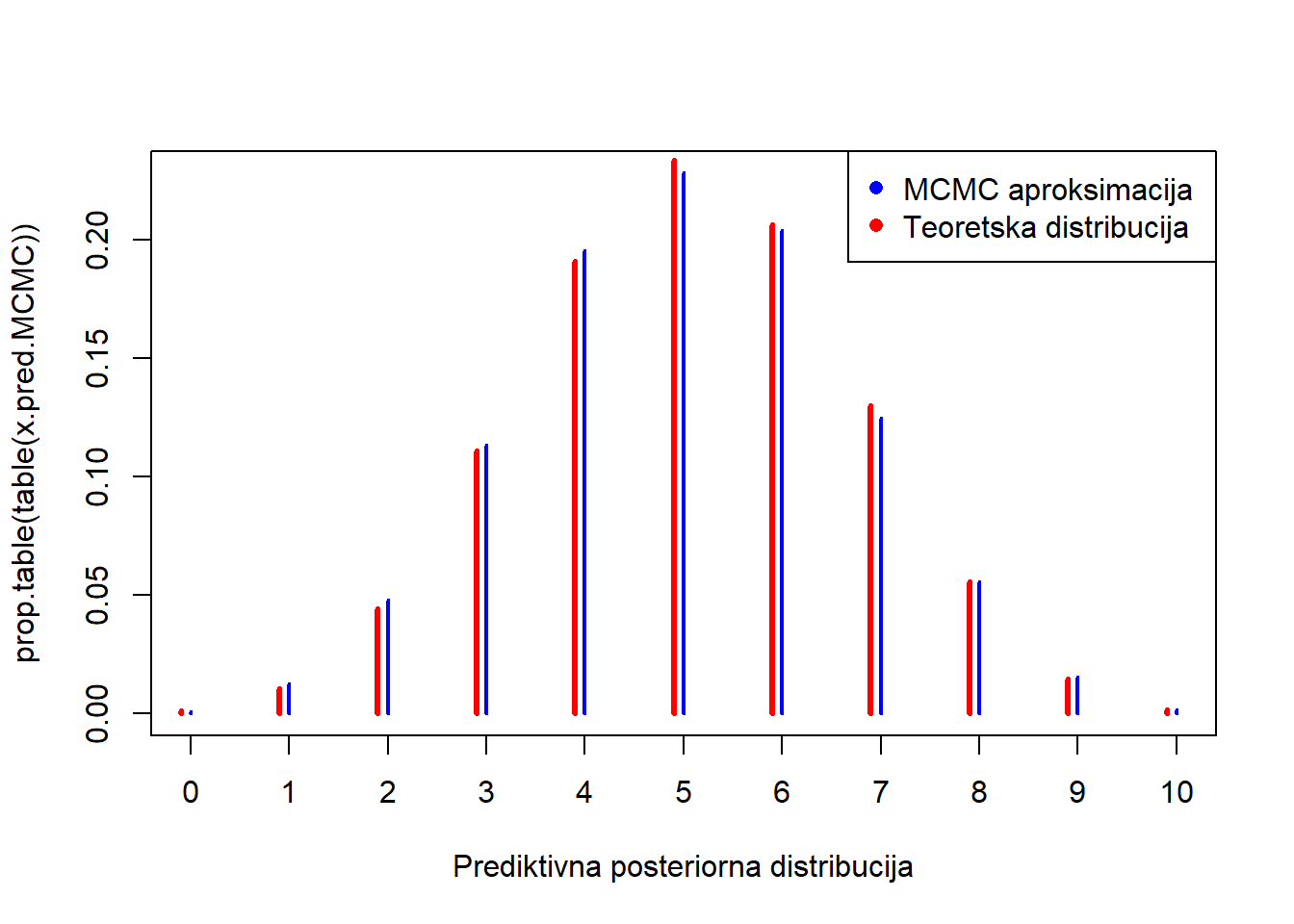
Zadatak 5.6 Neka je zadan miješani model tri normalne distribucije \[\begin{align*} \theta | &\delta \sim \mathcal{N}(\mu_{\delta}, \sigma^2_{\delta}) \\ & \delta \sim \left( \begin{array}{ccc} 1 & 2 & 3 \\ 0.45 & 0.1 & 0.45 \end{array} \right) \\ & (\mu_1, \mu_2, \mu_3 )=(-3,0,3), \quad (\sigma^2_1, \sigma^2_2, \sigma^2_3)= (1/3, 1/3, 1/3). \end{align*}\]
- Grafički prikažite gustoću modela.
- Generirajte uzorak dimenzije \(S=2000\) za \((\theta, \delta)\) korištenjem Monte Carlo (MC) metode. Na temelju MC aproksimacije grafički usporedite marginalnu teorijsku distribuciju za \(\theta\) sa pripadnom aproksimacijom.
- Generirajte uzorak dimenzije \(S=10000\) za \((\theta, \delta)\) korištenjem metode Monte Carlo Markovljevih lanaca (MCMC metode) uz početnu vrijednost \(\theta=0\). Na temelju MCMC aproksimacije grafički usporedite marginalnu teorijsku distribuciju za \(\theta\) sa pripadnom aproksimacijom.
- Koja aproksimacija daje bolje rezultate. Zašto?
- Generirajte novu MCMC aproksimaciju s početnom vrijednosti \(\theta=-6\).
- Odredite efektivnu veličinu uzorka za MCMC metodu te autokorelaciju dobivenog uzorka za \(\theta\) na lagu 10 i 50. Komentirajte.
mu<-c(-3,0,3)
s2<-c(.33,.33,.33)
w<-c(.45,.1,.45)
ths<-seq(-5,5,length=100)
plot(ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])) ,type="l", ylab="" )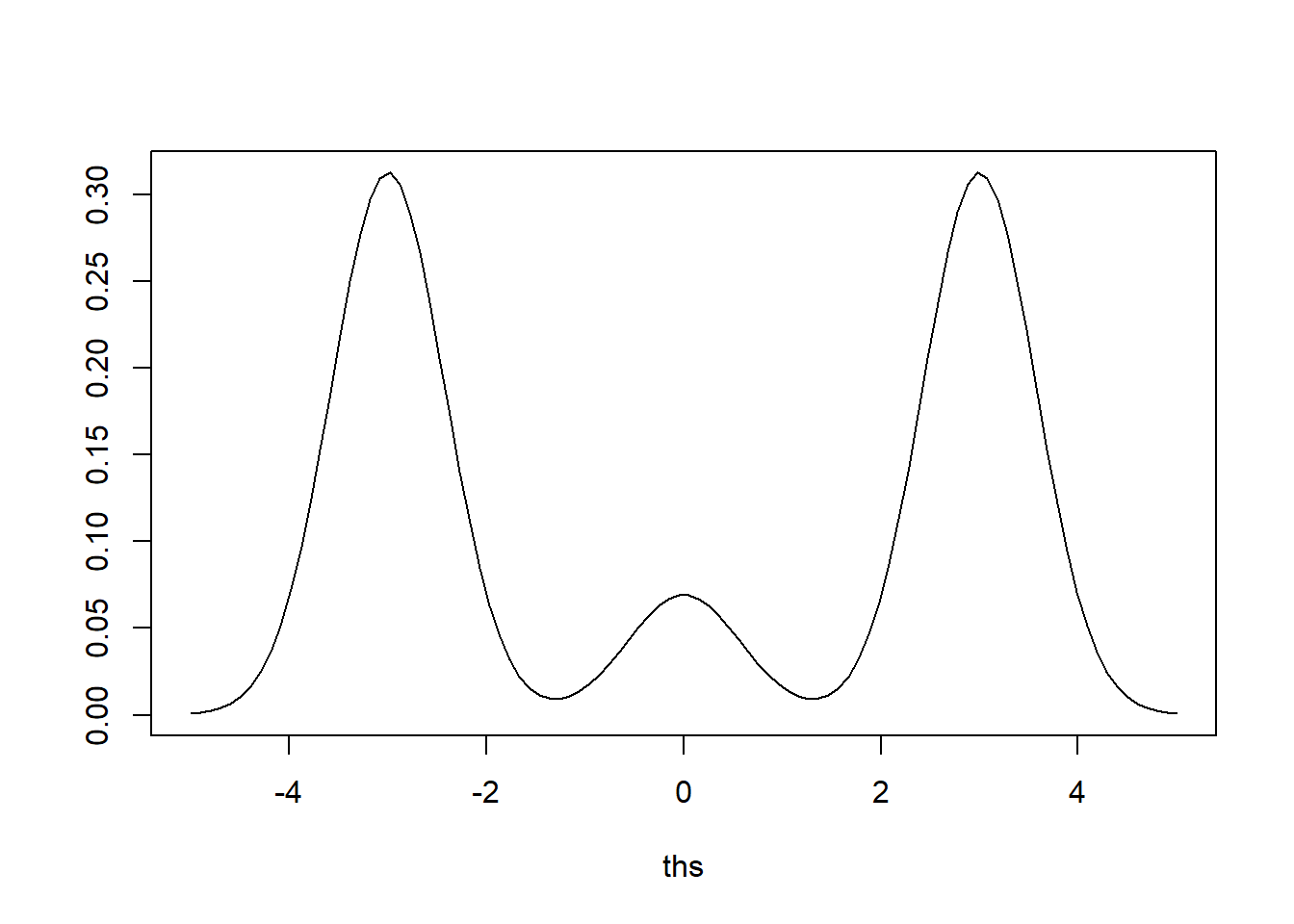
- Uzorkovanje MC metodom podrazumijeva da znamo generirati vrijednosti izravno iz tražene distribucije \(f(\theta, \delta)\). Ovdje to možemo (neposredno) napraviti jer je \[f(\theta, \delta)=f(\theta | \delta ) \cdot f(\delta)\]
S<-2000
d<-sample(1:3,S, prob=w,replace=TRUE)
th<-rnorm(S,mu[d],sqrt(s2[d]))
THD.MC<-cbind(th,d)Grafički prikaz:
par(mfrow=c(1,2),mar=c(3,3,1,1),mgp=c(1.75,.75,0))
ths<-seq(-6,6,length=1000)
plot(ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])) ,type="l" ,
xlab=expression(theta),ylab=
expression( paste( italic("p("),theta,")",sep="") ),lwd=2 ,ylim=c(0,.40))
hist(THD.MC[,1],add=TRUE,prob=TRUE,nclass=20,col="gray")
lines( ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])),lwd=2 )
plot(THD.MC[1:2000,1],xlab="iteration",ylab=expression(theta))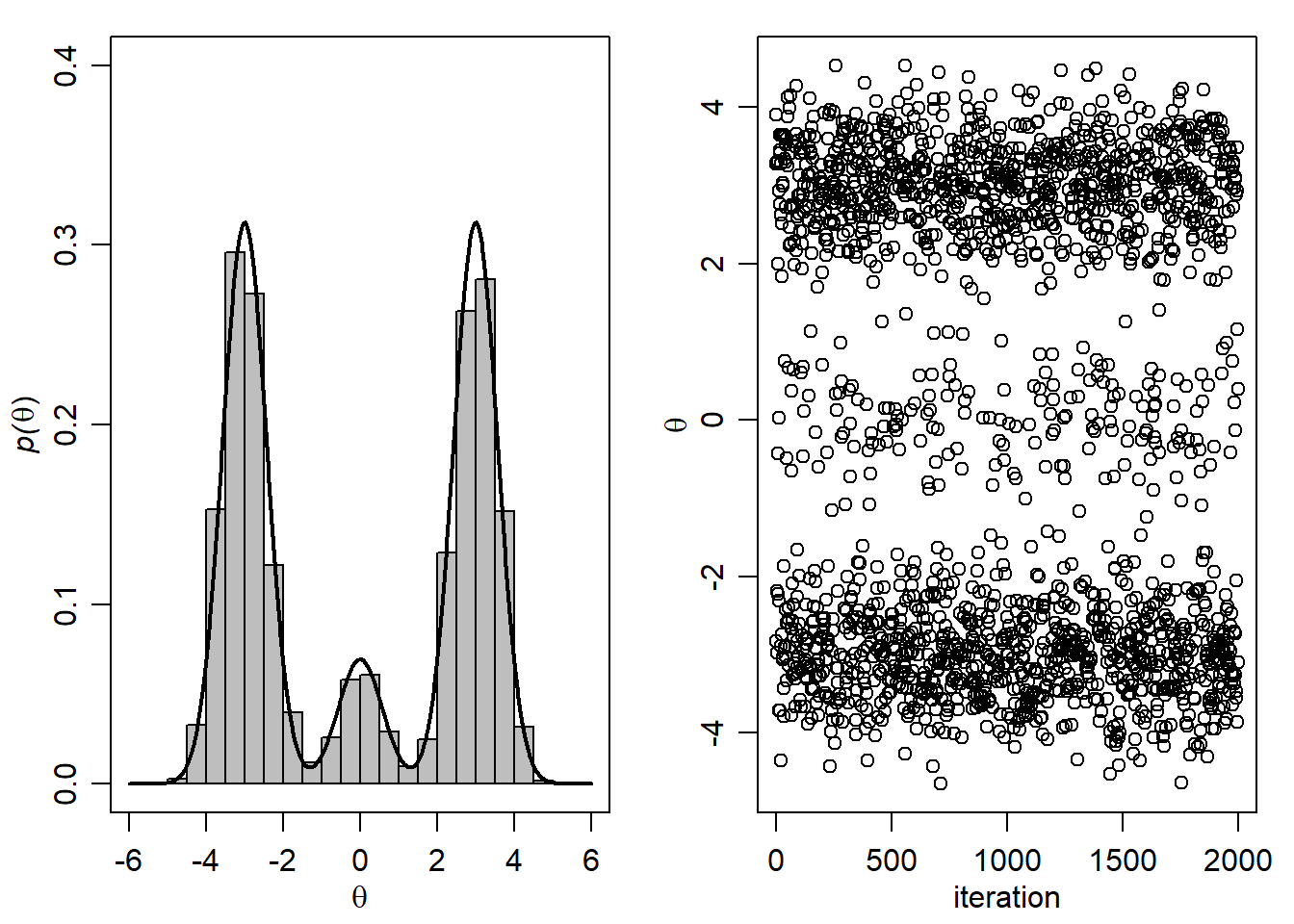
- MCMC metoda (Gibbsovo uzorkovanje) podrazumijeva generiranje vrijednosti iz uvjetnih distribucija parametra, tj. najprije generiramo iz
\[f(\delta | \theta)=\frac{f(\theta|\delta)\cdot f(\delta)}{\sum_{i=1}^{3}f(\theta|\delta_i)\cdot f(\delta_i)}\] a zatim korištenjem simuliranog \(\delta\) generiramo \(\theta\) iz uvjetne distribucije \[f(\theta | \delta).\]
th<-0
THD.MCMC<-NULL
S<-10000
for(s in 1:S) {
d<-sample(1:3 ,1,prob= w*dnorm(th,mu,sqrt(s2)) )
th<-rnorm(1,mu[d],sqrt(s2[d]) )
THD.MCMC<-rbind(THD.MCMC,c(th,d) )
}Grafički prikaz:
par(mfrow=c(1,2),mar=c(3,3,1,1),mgp=c(1.75,.75,0))
Smax<-1000
ths<-seq(-6,6,length=1000)
plot(ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])) ,type="l" , xlab=expression(theta),
ylab=expression( paste( italic("p("),theta,")",sep="") ),lwd=2 ,ylim=c(0,.40))
hist(THD.MCMC[1:10000,1],add=TRUE,prob=TRUE,nclass=20,col="gray")
lines( ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])),lwd=2 )
plot(THD.MCMC[1:10000,1],xlab="iteration",ylab=expression(theta))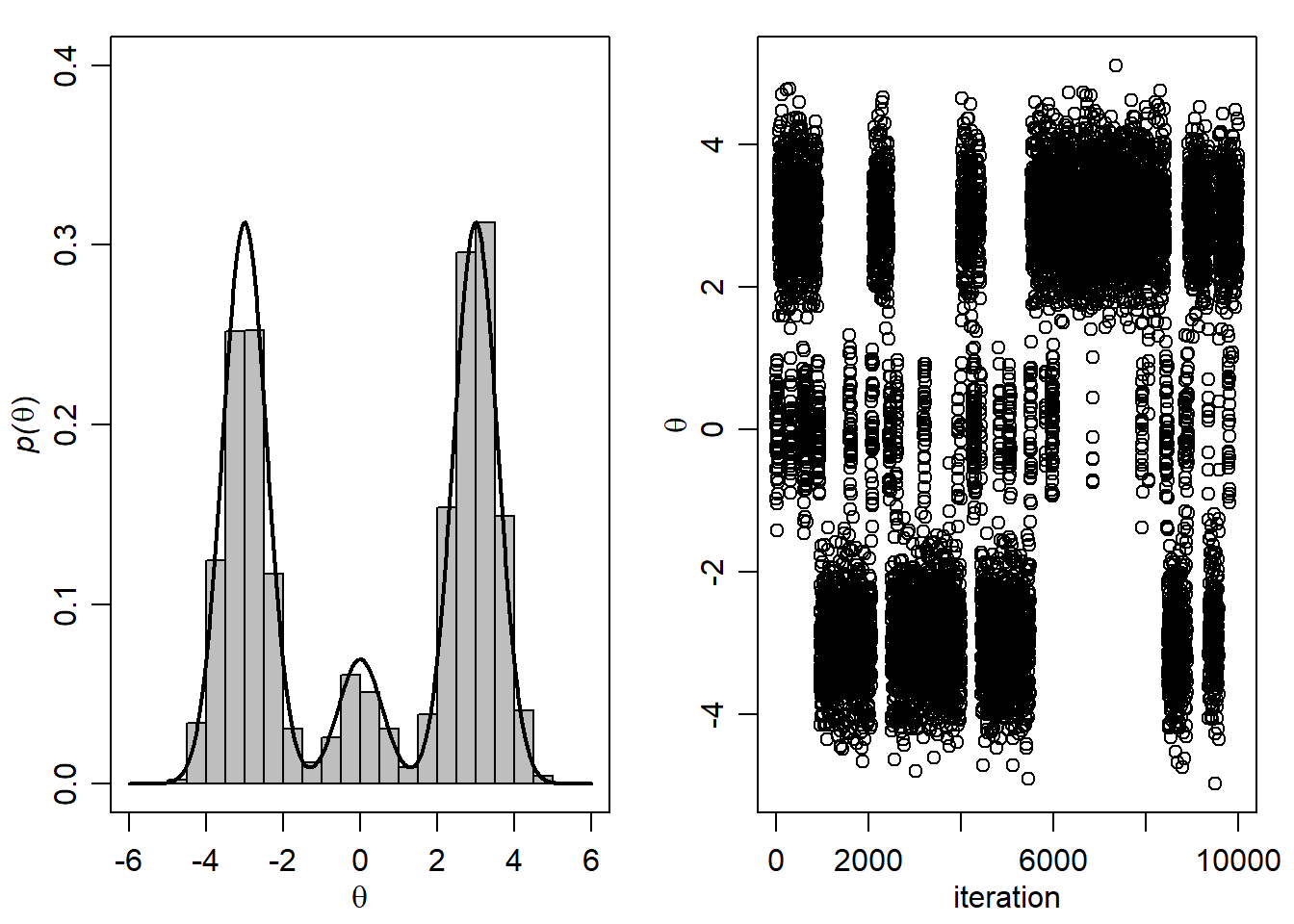
MC metoda daje bolje rezultate u odnosu na MCMC metodu (Gibbsovo uzorkovanje) unatoč tome što je MC metoda bazirana na \(S=2000\), a MCMC metoda na \(S=10000\) vrijednosti. Naime, uzorak dobiven MCMC metodom je snažno koreliran niz vrijednosti (bazira se na Markovljevom lancu), dok uzorak generiran standardnom MC metodom nema strukturu zavisnosti, tj. sve vrijednosti \[(\theta^{(1)}, \delta^{(1)}), \dots, (\theta^{(S)}, \delta^{(S)})\] su nezavisno generirane .
th<--6
THD.MCMC<-NULL
S<-10000
for(s in 1:S) {
d<-sample(1:3 ,1,prob= w*dnorm(th,mu,sqrt(s2)) )
th<-rnorm(1,mu[d],sqrt(s2[d]) )
THD.MCMC<-rbind(THD.MCMC,c(th,d) )
}Grafički prikaz:
par(mfrow=c(1,2),mar=c(3,3,1,1),mgp=c(1.75,.75,0))
Smax<-1000
ths<-seq(-6,6,length=1000)
plot(ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])) ,type="l" , xlab=expression(theta),
ylab=expression( paste( italic("p("),theta,")",sep="") ),lwd=2 ,ylim=c(0,.40))
hist(THD.MCMC[1:10000,1],add=TRUE,prob=TRUE,nclass=20,col="gray")
lines( ths, w[1]*dnorm(ths,mu[1],sqrt(s2[1])) +
w[2]*dnorm(ths,mu[2],sqrt(s2[2])) +
w[3]*dnorm(ths,mu[3],sqrt(s2[3])),lwd=2 )
plot(THD.MCMC[1:10000,1],xlab="iteration",ylab=expression(theta))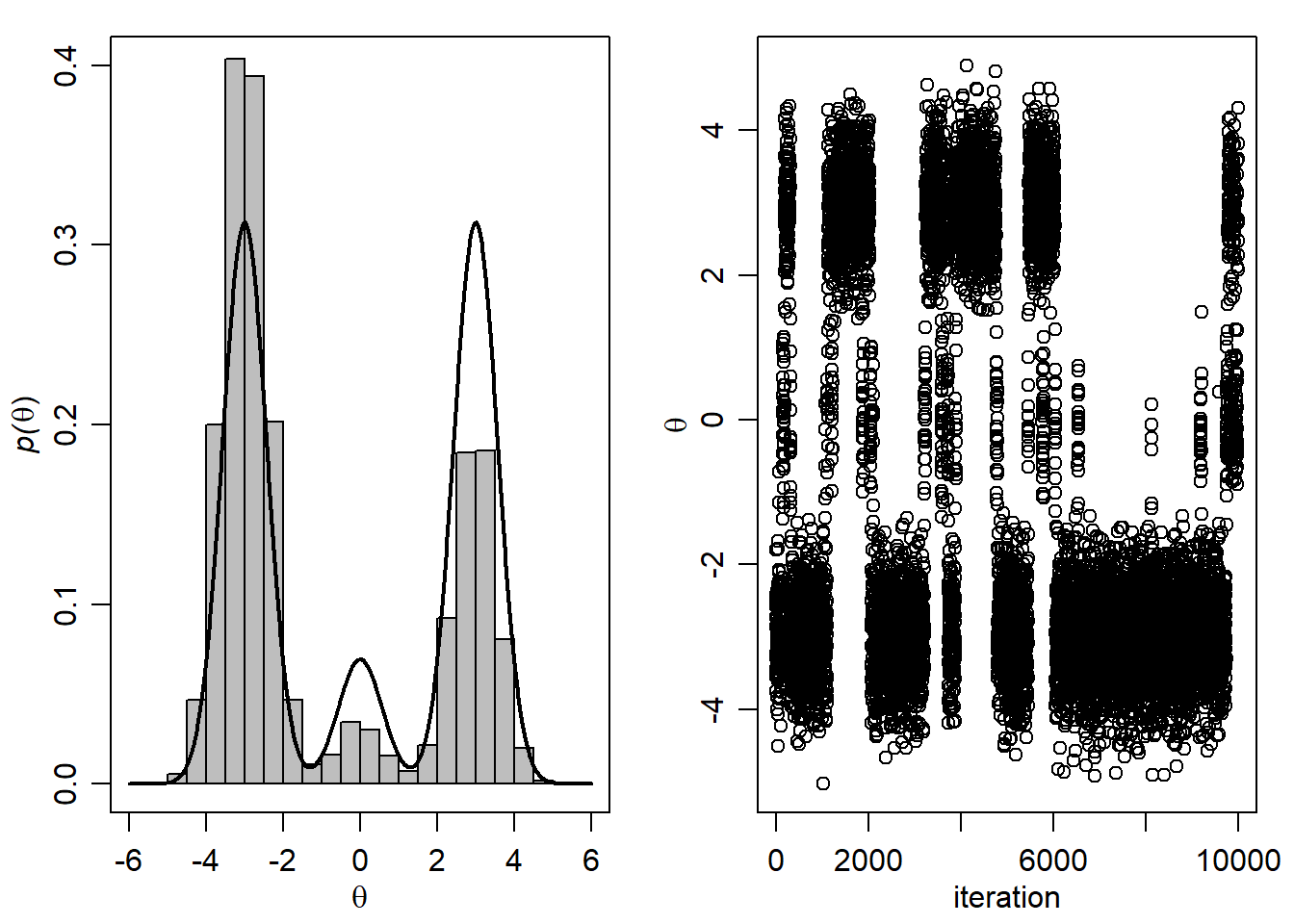
Možemo primijetiti da je odabir početne vrijednosti \(\theta=-6\) posljedično značio veću zastupljenost “lijeve” regije te je usporilo konvergenciju Markovljevog lanca. Idealno bi bilo započinjati Gibbsovo uzorkovanje u području s velikom vjerojatnošću (iako to u praksi ne znamo, možemo samo naslutiti).
- Efektivna veličina uzorka iznosi
effectiveSize(THD.MCMC[,1]) var1
14.92217 acf(THD.MCMC[,1], lag=50)[c(10,50)]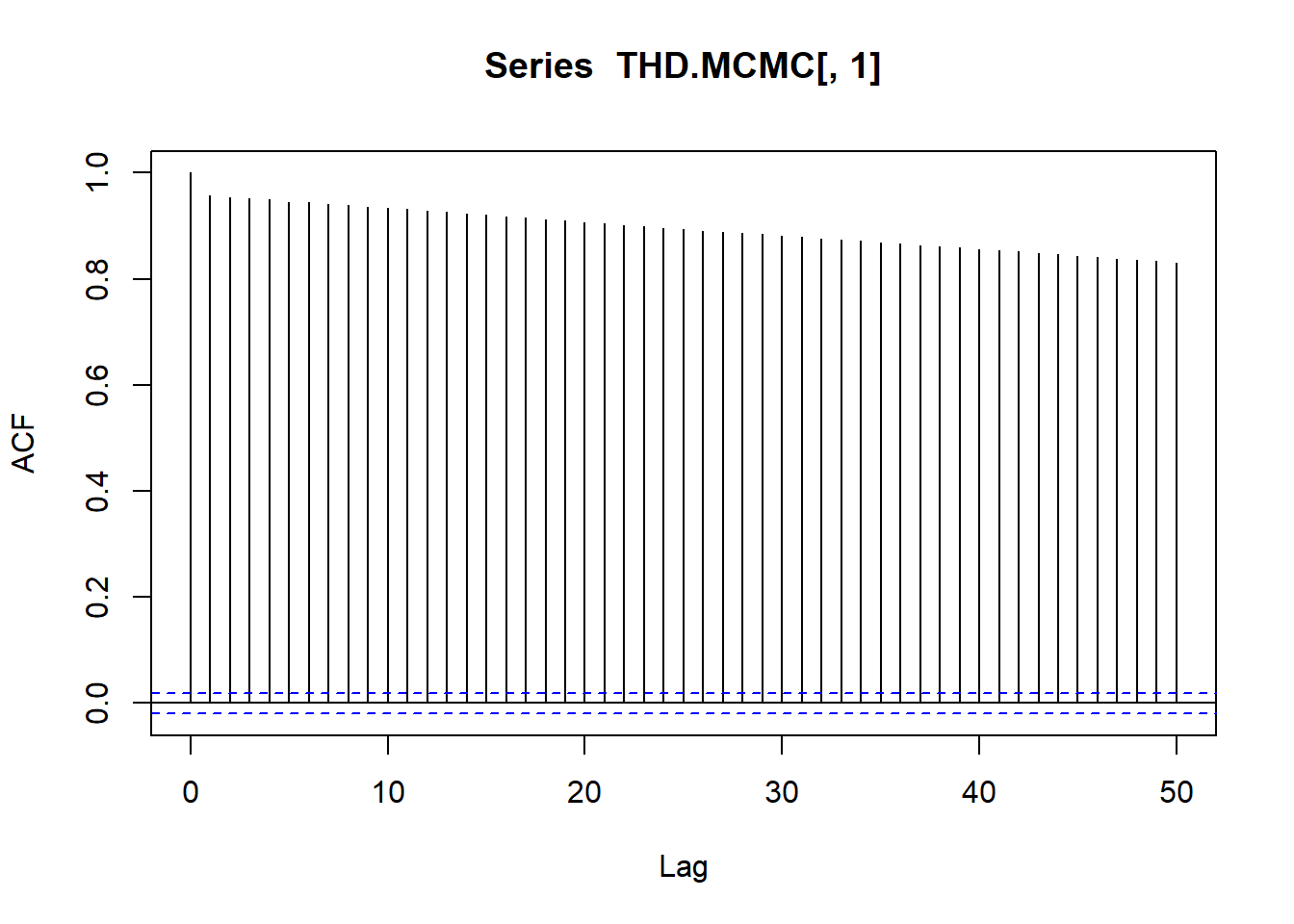
Autocorrelations of series 'THD.MCMC[, 1]', by lag
10 50
0.933 0.831 dok je autokorelacija na lagu 10 \(0.933\), a na lagu 50 \(0.831.\) Dakle, kvaliteta od MCMC aproksimacije dimenzije \(S=10000\) ekvivalentna je aproksimaciji dobivenoj MC metodom dimenzije \(S=15\). Uočavamo da se radi o značajnoj korelaciji u lancu, što sugerira sporu konvergenciju lanca prema traženoj distribuciji.
Zadatak 5.7 Riješite zadatke 5.4 i 5.5 MCMC metodom koristeći STAN platformu.
Zadatak 5.4
-a)
modelGamaExp <- "
data {
real <lower = 0> x[6]; // podaci
}
parameters {
real<lower = 0> lambda; // lambda
}
model {
x ~ exponential(lambda); // vjerodostojnost
lambda ~ gamma(1, 2); // apriorna distribucija
}
generated quantities {
real<lower = 0> x_tilda = exponential_rng(lambda);
}
"
podaci <- list(x=c(0.7, 1.2, 1.05, 0.9, 0.8, 1.1))
sim.MCMC.stan <-stan(
model_code = modelGamaExp,
data = podaci, # named list of data
chains = 4, # broj korištenih Markovljevih lanaca
warmup = 10000, # burn-in period
iter = 20000, # ukupan broj iteracija po Markovljevom lancu
cores = 1, # broj jezgri
refresh = 0, # bez prikazivanja napretka
seed=934
)
plot(sim.MCMC.stan) #crta vjerodostojne intervaleci_level: 0.8 (80% intervals)outer_level: 0.95 (95% intervals)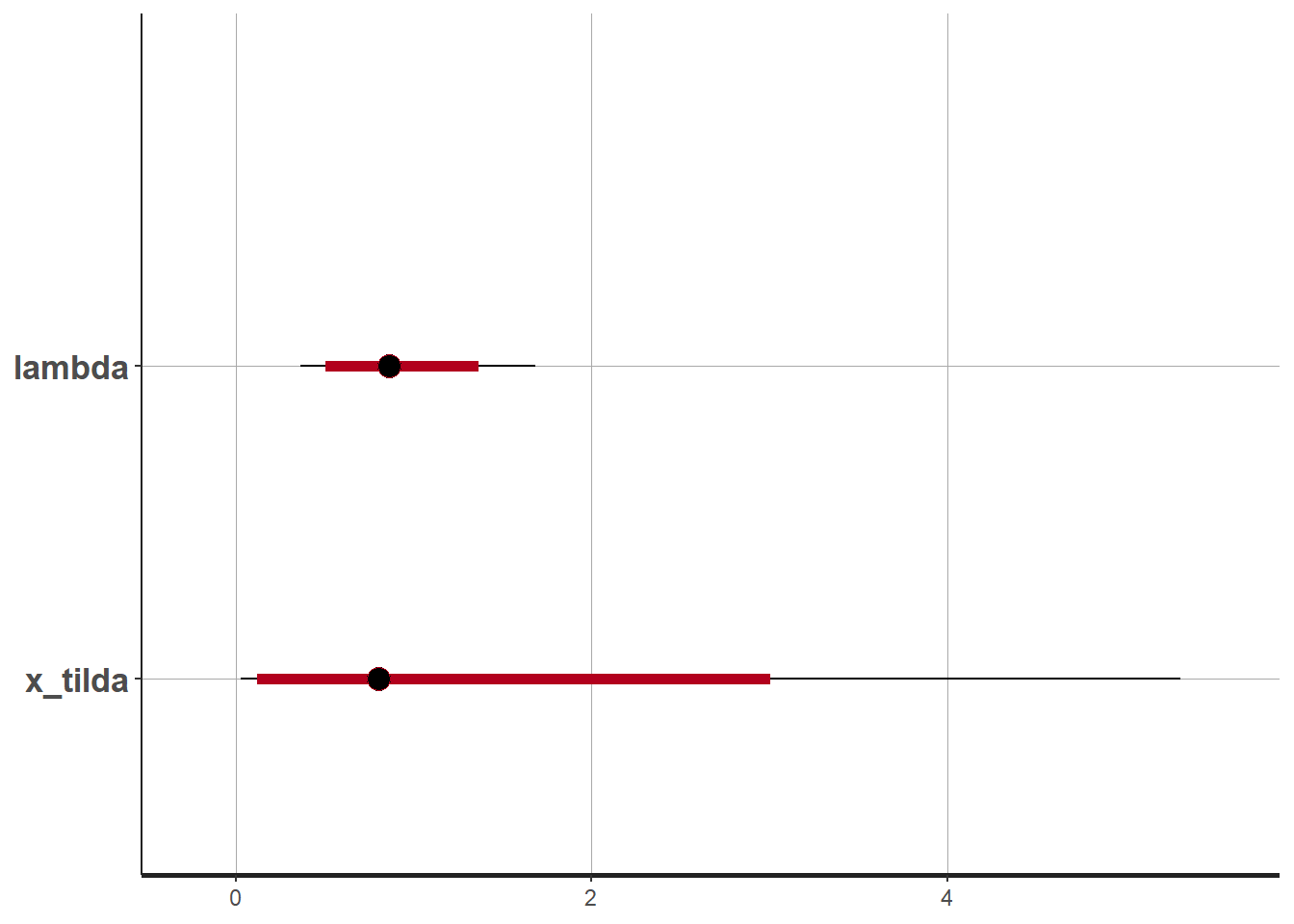
print(sim.MCMC.stan) #informacije o MCMC aproksimacijiInference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
lambda 0.91 0.00 0.34 0.37 0.65 0.86 1.11 1.68 13683 1
x_tilda 1.29 0.01 1.54 0.03 0.32 0.80 1.70 5.31 29310 1
lp__ -8.23 0.01 0.72 -10.28 -8.39 -7.95 -7.77 -7.71 14057 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:34:14 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).MCMC <- rstan::extract(sim.MCMC.stan, permuted = TRUE) #dohvacanje simuliranih vrijednosti
#parametra
plot(density(MCMC$lambda), col="blue", xlab="Posteriorna distribucija")
curve(dgamma(x,7, 7.75), add=T, col="red")
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 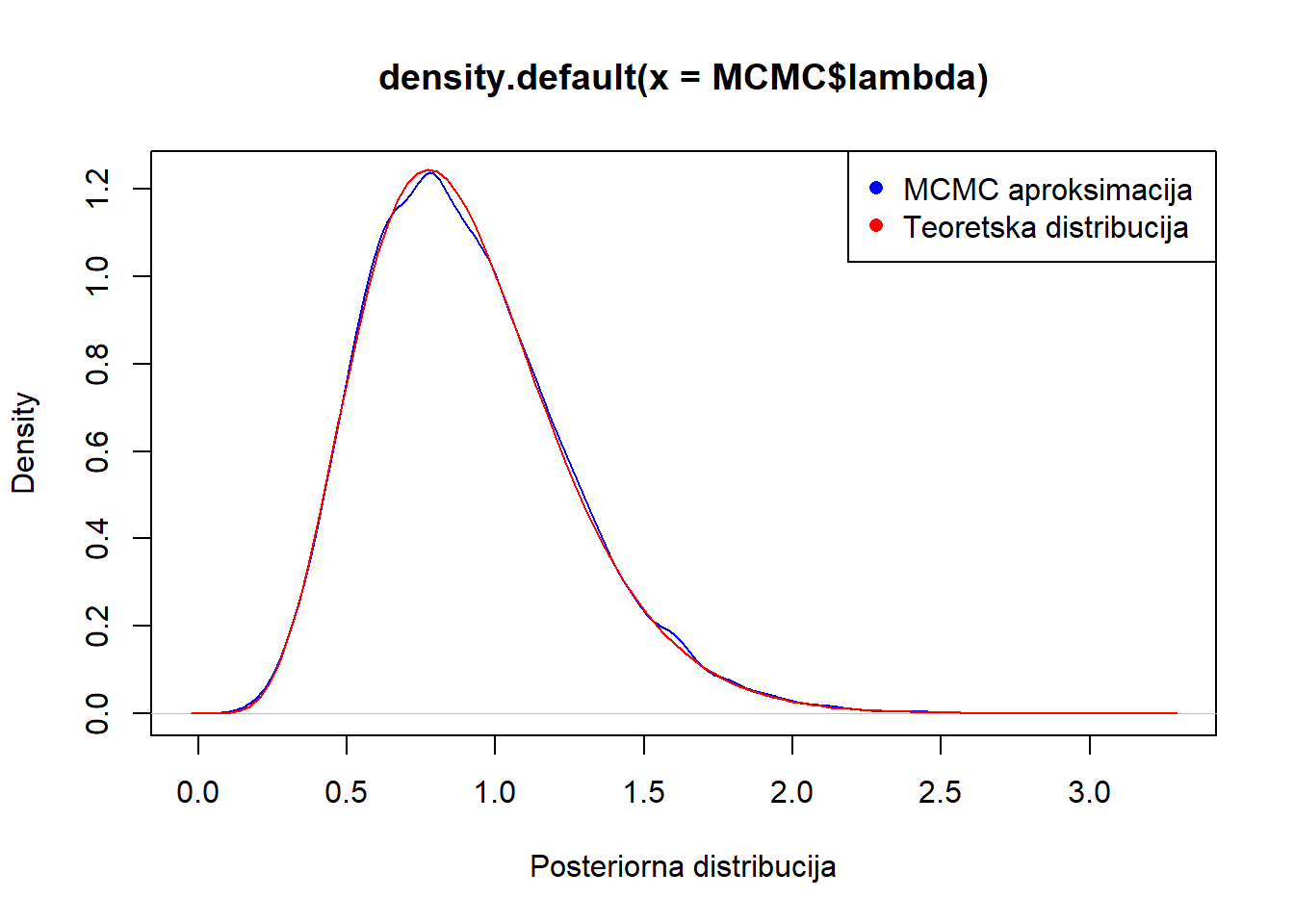
-b) plot(density(MCMC$x_tilda), col="blue", xlab="Prediktivna posteriorna distribucija")
curve(dlomax(x,1/(7.5),7), add=T, col="red")
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 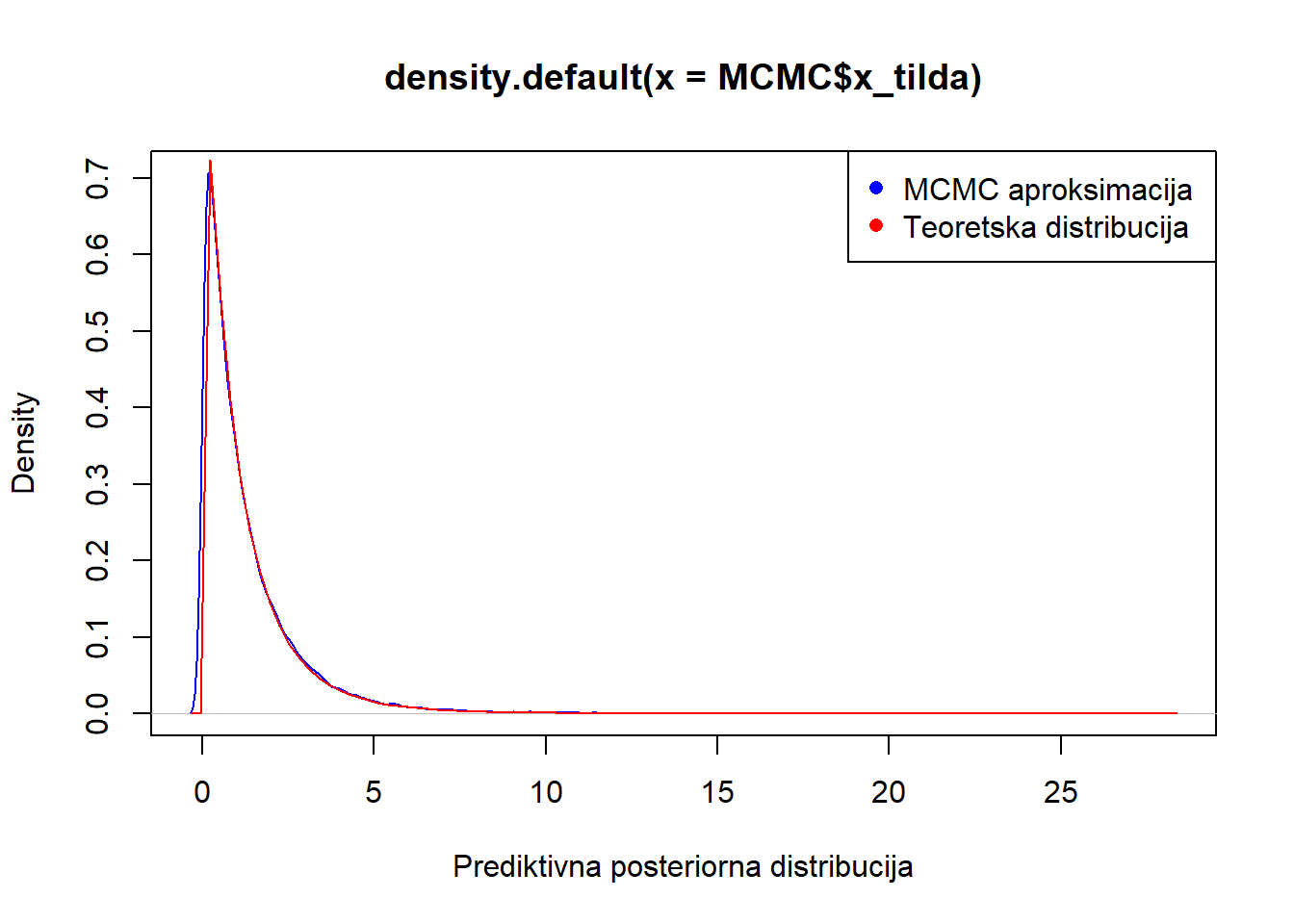
Zadatak 5.5
-a)
modelBetaBin <- "
data {
int <lower = 0, upper=10> x[9]; // podaci
}
parameters {
real<lower = 0, upper=1> theta; // parametar theta
}
model {
x ~ binomial(10,theta); // vjerodostojnost
theta ~ beta(2, 2); // apriorna distribucija
}
generated quantities {
int<lower = 0, upper=10> x_tilda = binomial_rng(10, theta);
}
"
podaci <- list(x=c(3,7,5,4,7,9,4,5,2))
sim.MCMC.stan <-stan(
model_code = modelBetaBin,
data = podaci, # named list of data
chains = 4, # broj korištenih Markovljevih lanaca
warmup = 10000, # burn-in period
iter = 20000, # ukupan broj iteracija po Markovljevom lancu
cores = 1, # broj jezgri
refresh = 0, # bez prikazivanja napretka
seed=934
)
plot(sim.MCMC.stan) #crta vjerodostojne intervaleci_level: 0.8 (80% intervals)outer_level: 0.95 (95% intervals)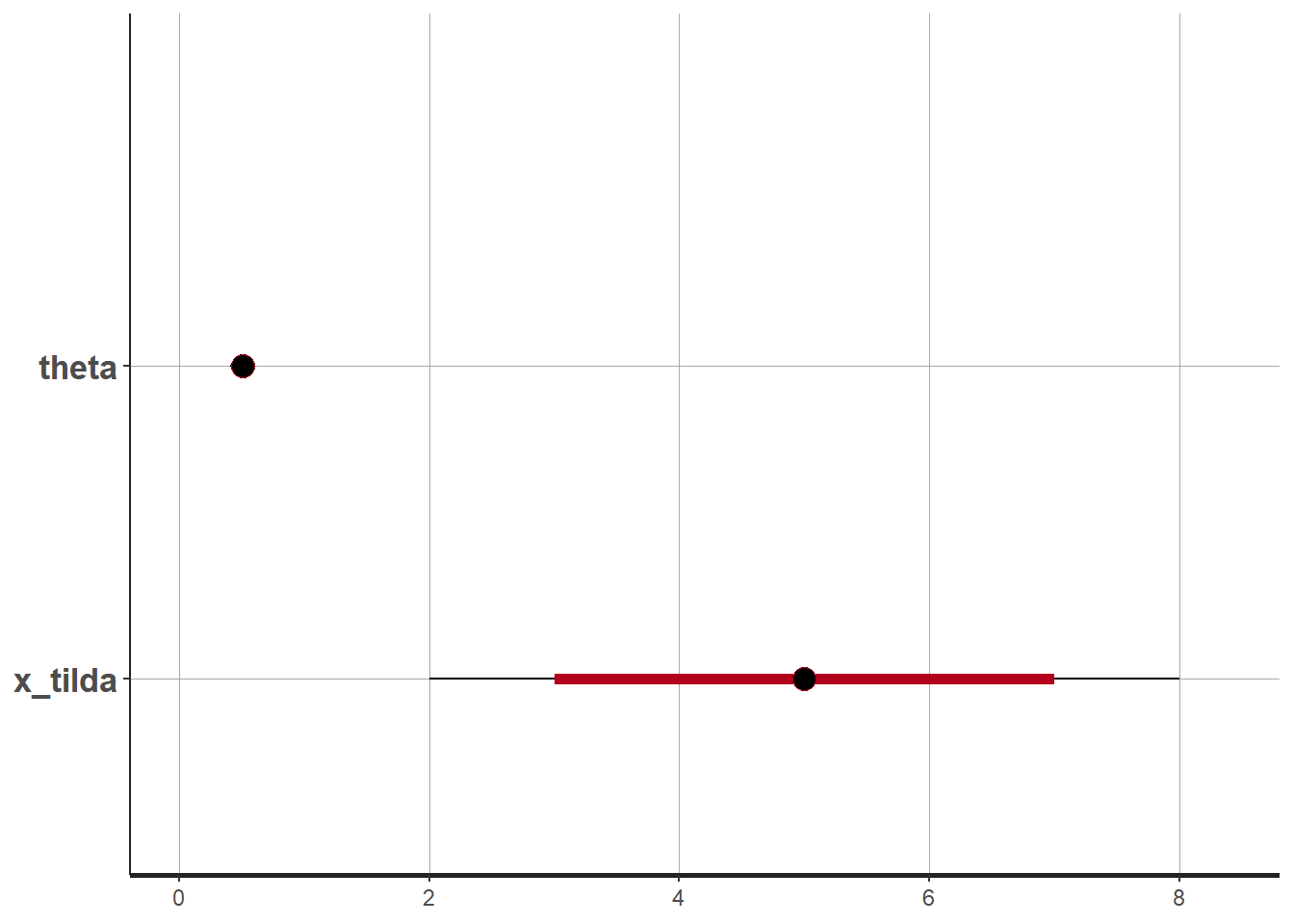
print(sim.MCMC.stan) #informacije o MCMC aproksimacijiInference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta 0.51 0.00 0.05 0.41 0.48 0.51 0.55 0.61 14968 1
x_tilda 5.11 0.01 1.65 2.00 4.00 5.00 6.00 8.00 35039 1
lp__ -65.64 0.01 0.72 -67.70 -65.79 -65.36 -65.18 -65.13 16408 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:34:58 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).MCMC <- rstan::extract(sim.MCMC.stan, permuted = TRUE) #dohvacanje simuliranih vrijednosti
#parametra
plot(density(MCMC$theta), col="blue", xlab="Posteriorna distribucija")
curve(dbeta(x,48, 46), add=T, col="red")
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 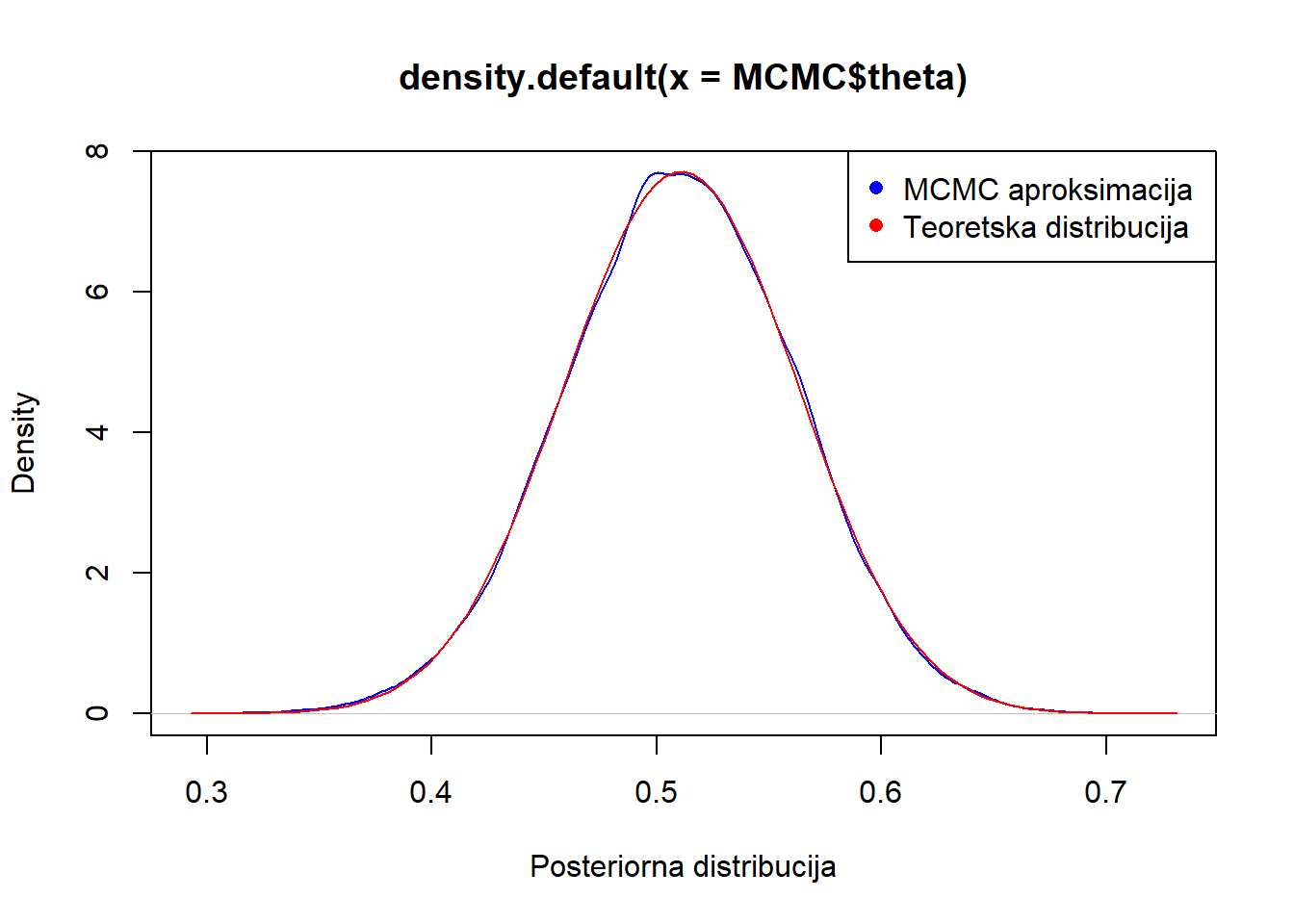
-b) plot(prop.table(table(MCMC$x_tilda)), col="blue", xlab="Prediktivna posteriorna distribucija")
points(c(0:10)-0.1, dbbinom(c(0:10), 10, 48, 46), col="red" ,type="h",
ylab=expression(paste(italic("p("),y[n+1],"|",y[1],"...",y[n],")",sep="")),
xlab=expression(italic(y[n+1])),ylim=c(0,.5),lwd=3)
legend("topright", legend = c("MCMC aproksimacija ", "Teoretska distribucija"), col = c("blue", "red"), pch = c(16, 16)) 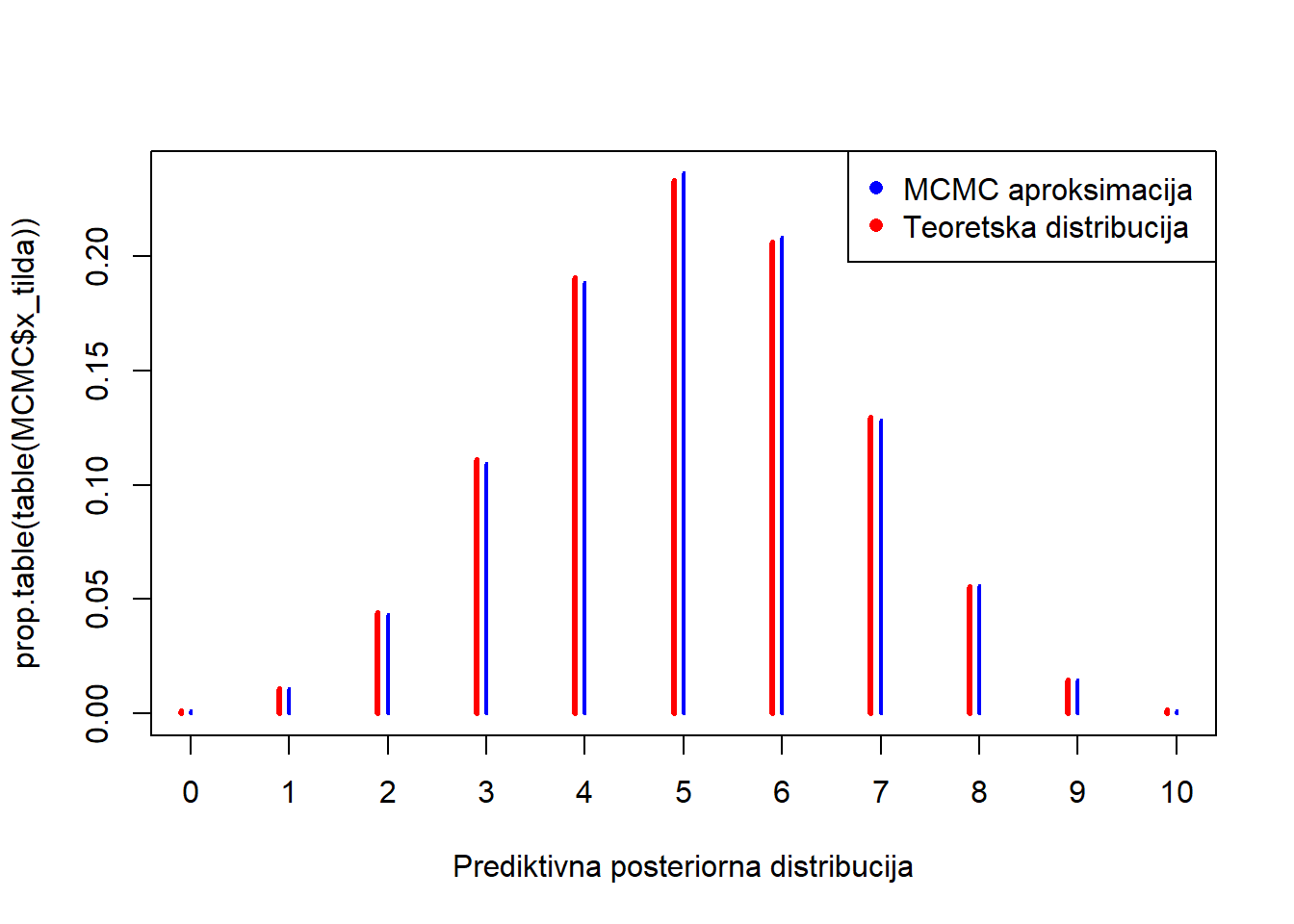
Zadatak 5.8 U bazi podataka midge (iz paketa Flury) nalaze se podaci o duljini krila dviju vrsta mušica (Amerohelea fasciata (Af) i Pseudofasciata (Apf)). Pretpostavka je da mjerenja dolaze iz normalne distribucije. Prethodna istraživanja sugeriraju da je očekivana duljina krila za mušice \(1.9 mm\) uz standardnu devijaciju \(0.1\)
- Napravite aproksimaciju posteriorne distribucije parametara za mušicu vrste Apf MCMC metodom koristeći STAN platformu. Pri tome koristite 4 Markovljeva lanca dimenzije 20000, pri čemu polovicu simulacija koristite kao “burn-in” period.
- Analizirajte kvalitetu dobivene aproksimacije, odnosno je li korištena metoda konvergirala.
- Što možete reći o brzini miješanja dobivene aproksimacije?
- Koliko iznosi efektivna uzoračka veličina? Interpretirajte.
- Odredite posteriorne \(0.05\)-vjerodostojne intervale za očekivanja i varijance.
- Koliko iznosi vjerojatnost da slučajno odabrana mušica ove vrste ima duljinu krila između 1.8 mm i 2 mm?
- Ukoliko zanemarimo prethodna istraživanja kakve rezultate i procjene dobivamo?
- Model i implementacija MCMC metode korištenjem STAN platforme:
modelMusiceApf <- "
data {
real <lower = 0> x[6]; // podaci
}
parameters {
real mu; // parametar mu
real<lower = 0> sigma2; // parametar sigma2
}
model {
x ~ normal(mu,sqrt(sigma2)); // vjerodostojnost
mu ~ normal(1.9,0.1); //apriorna distribucija
}
generated quantities {
real x_tilda = normal_rng(mu,sqrt(sigma2));
}"
sim.MCMC.stan.Apf <-stan(
model_code = modelMusiceApf,
data = list(x=midge$Wing.Length[Species=="Apf"]), # named list of data
chains = 4, # broj korištenih Markovljevih lanaca
warmup = 10000, # burn in period za svaki lanac
iter = 20000, # ukupan broj iteracija svakog lanca
cores = 1, # broj korištenih jezgri
refresh = 0, # no progress show
seed=934
)Aproksimacija posteriorne distribucije za \(\mu\):
mcmc_dens(sim.MCMC.stan.Apf, pars = "mu") +
yaxis_text(TRUE) +
ylab("gustoća") 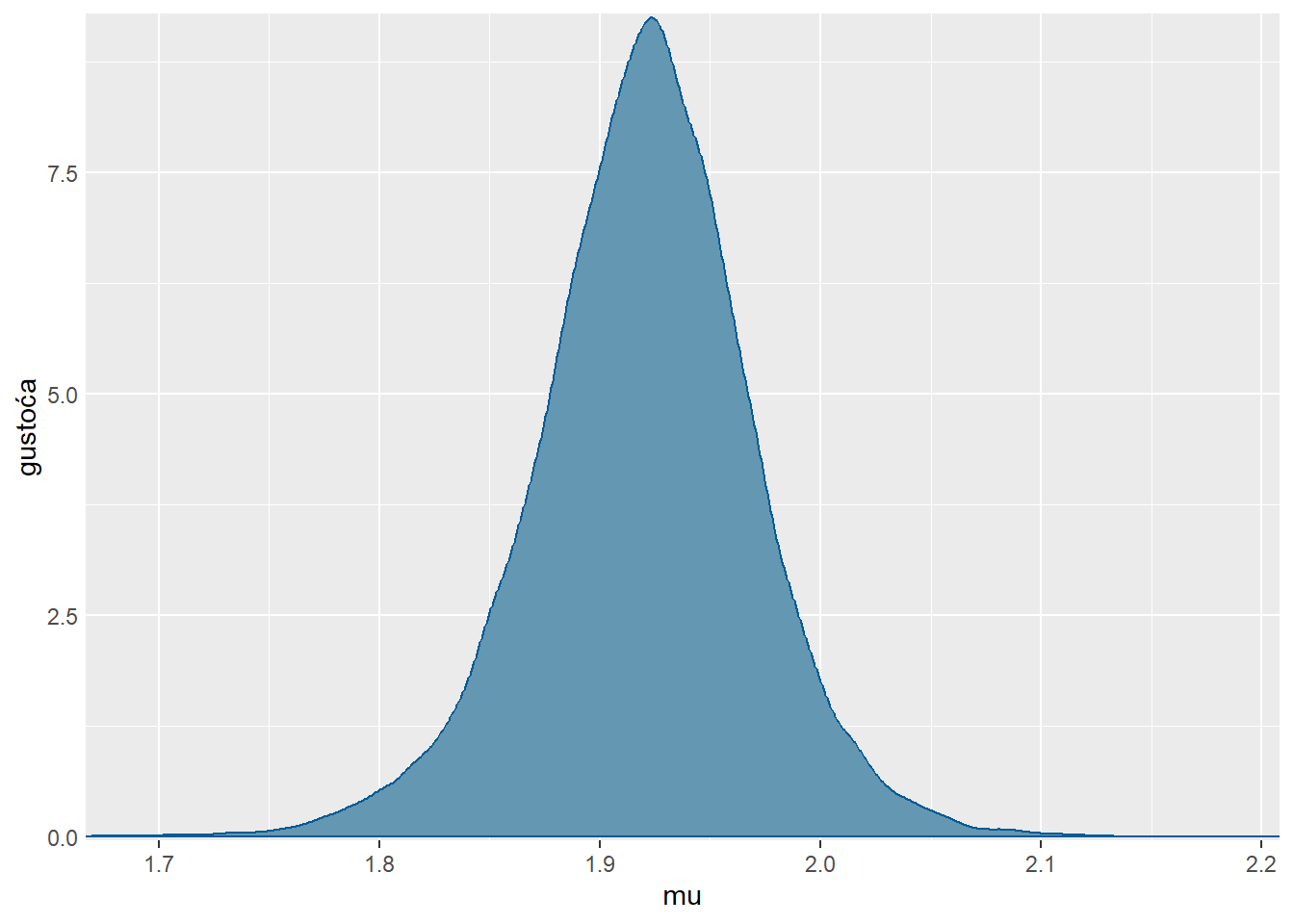
Aproksimacija posteriorne distribucije za \(\sigma^2\):
mcmc_dens(sim.MCMC.stan.Apf, pars = "sigma2") +
yaxis_text(TRUE) + xlim(0,1)+
ylab("gustoća") Scale for x is already present.
Adding another scale for x, which will replace the existing scale.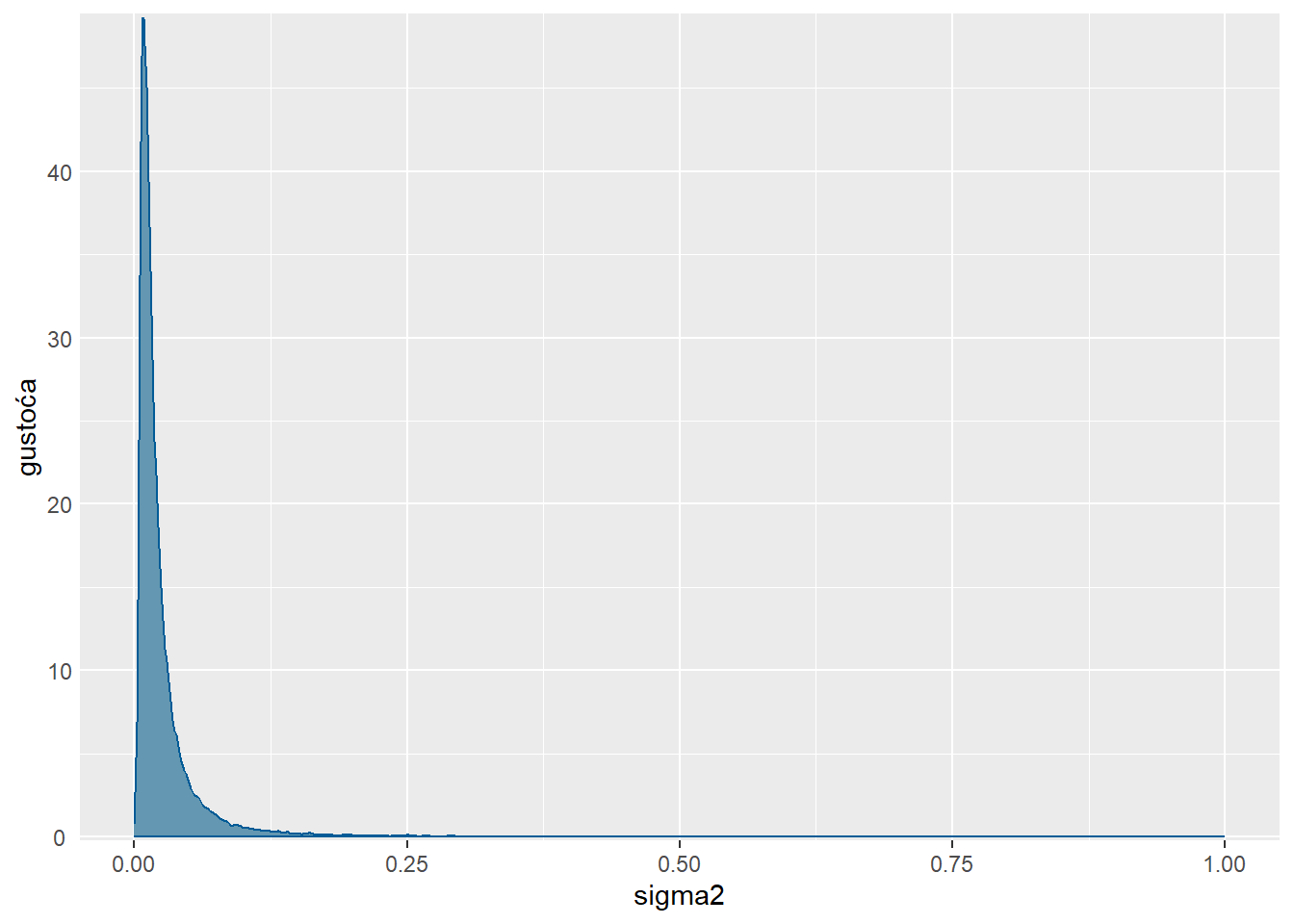
Sljedećom naredbom dobivamo pregled dobivene posteriorne aproksimacije (prosjek, standardna greška, standardna devijacija, kvantili, efektivna veličina uzorka, \(\hat{R}\) - u slučaju konvergenicije treba biti 1).
print(sim.MCMC.stan.Apf)Inference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 1.92 0.00 0.05 1.82 1.89 1.92 1.95 2.02 16453 1
sigma2 0.03 0.00 0.06 0.00 0.01 0.01 0.03 0.12 15596 1
x_tilda 1.92 0.00 0.17 1.58 1.83 1.92 2.01 2.26 36346 1
lp__ 6.07 0.01 1.12 3.07 5.61 6.41 6.89 7.20 11175 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:35:42 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).Usporedba trajektorija generiranih vrijednosti korištenjem četiriju lanaca:
mcmc_trace(sim.MCMC.stan.Apf, pars = "mu", size = 0.5) 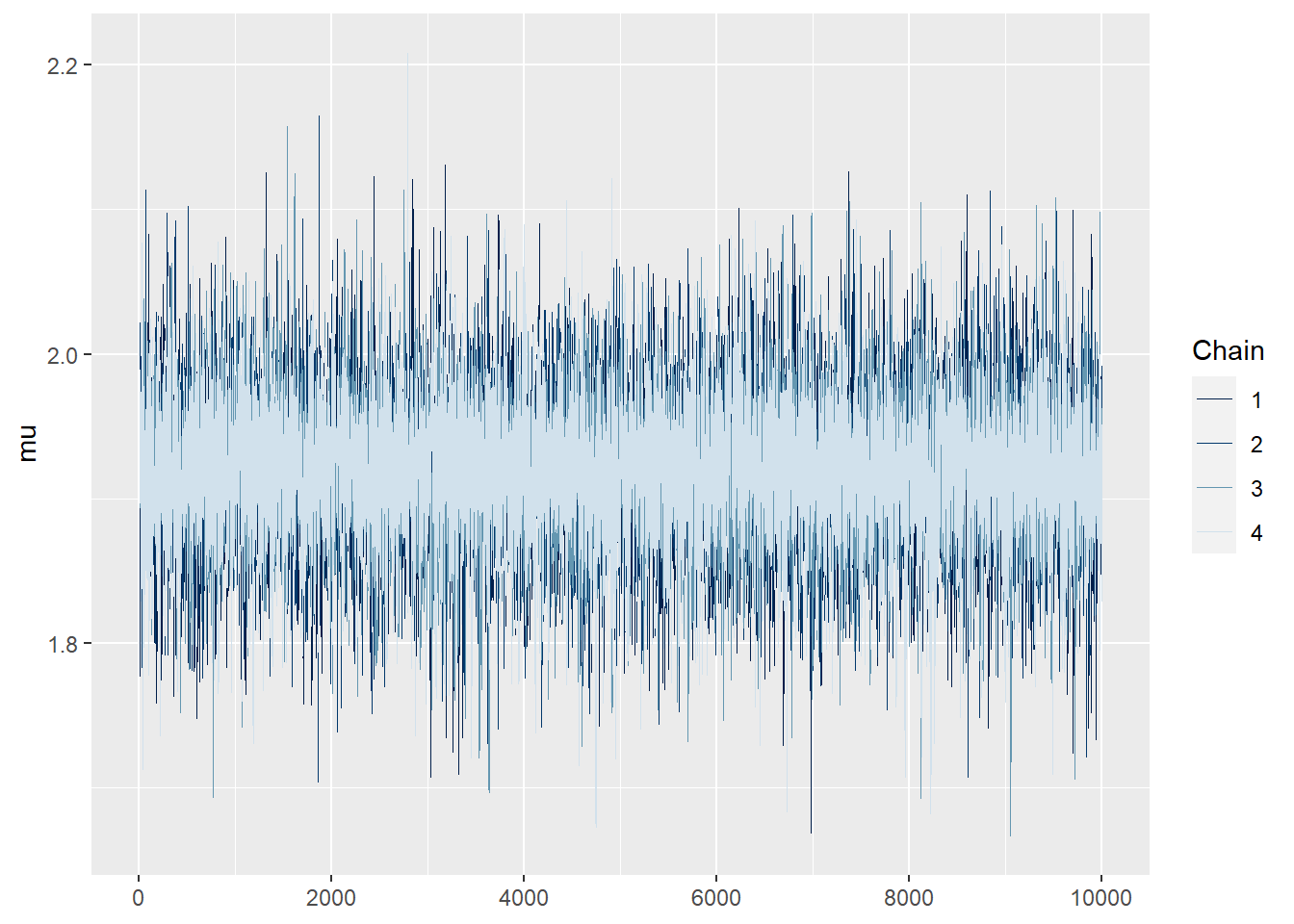
Ne uočavamo nikakve trendove niti strukturu u trajektorijama, sugerira konvergenciju.
Usporedba posteriornih distribucija četiriju lanaca:
mcmc_dens_overlay(sim.MCMC.stan.Apf , pars = "mu")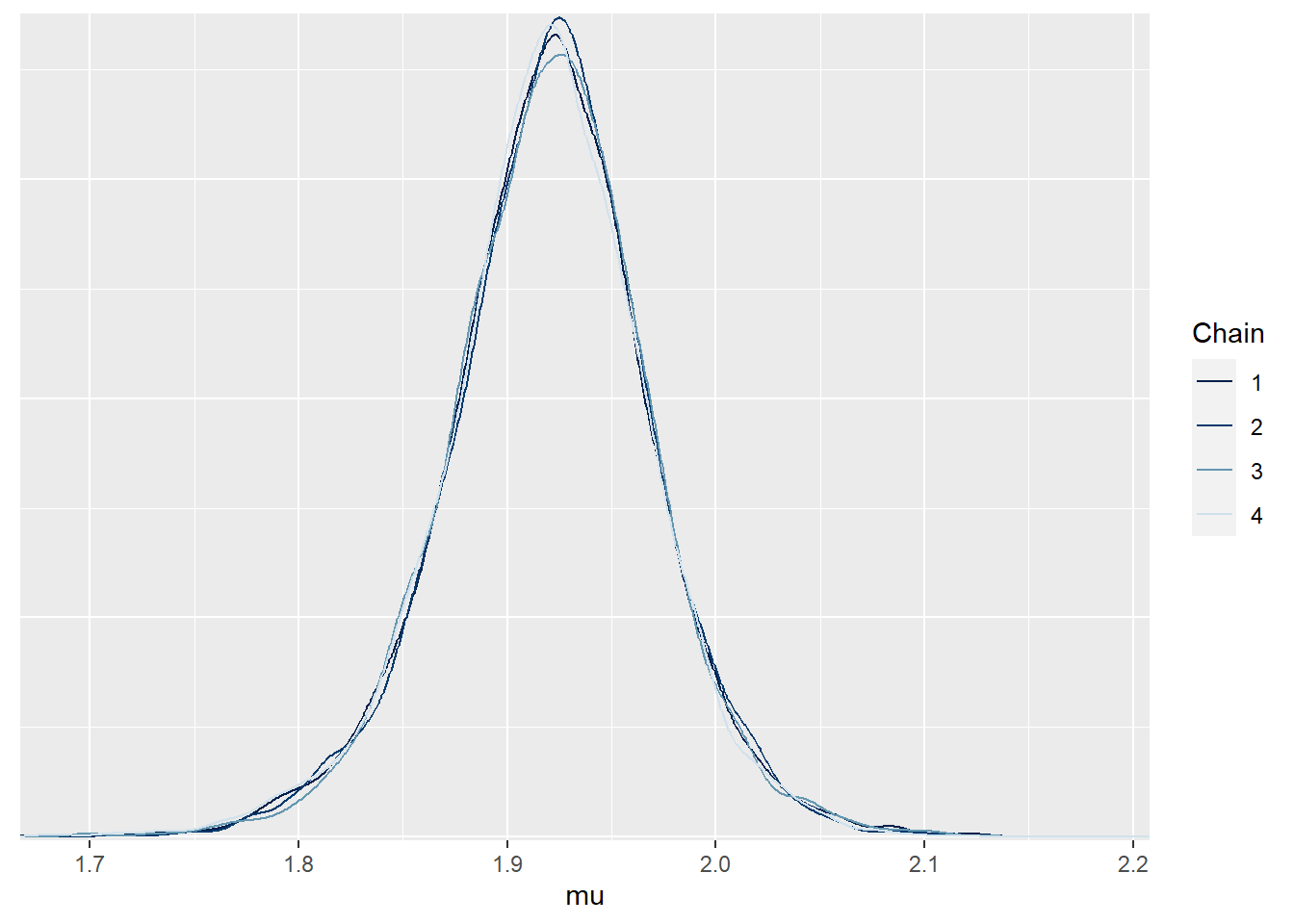
mcmc_dens_overlay(sim.MCMC.stan.Apf , pars = "sigma2")
Vidimo da su ujednačene što sugerira da je došlo do konvergencije.
Autokorelacijske funkcije četiriju lanaca:
mcmc_acf(sim.MCMC.stan.Apf, pars = "mu")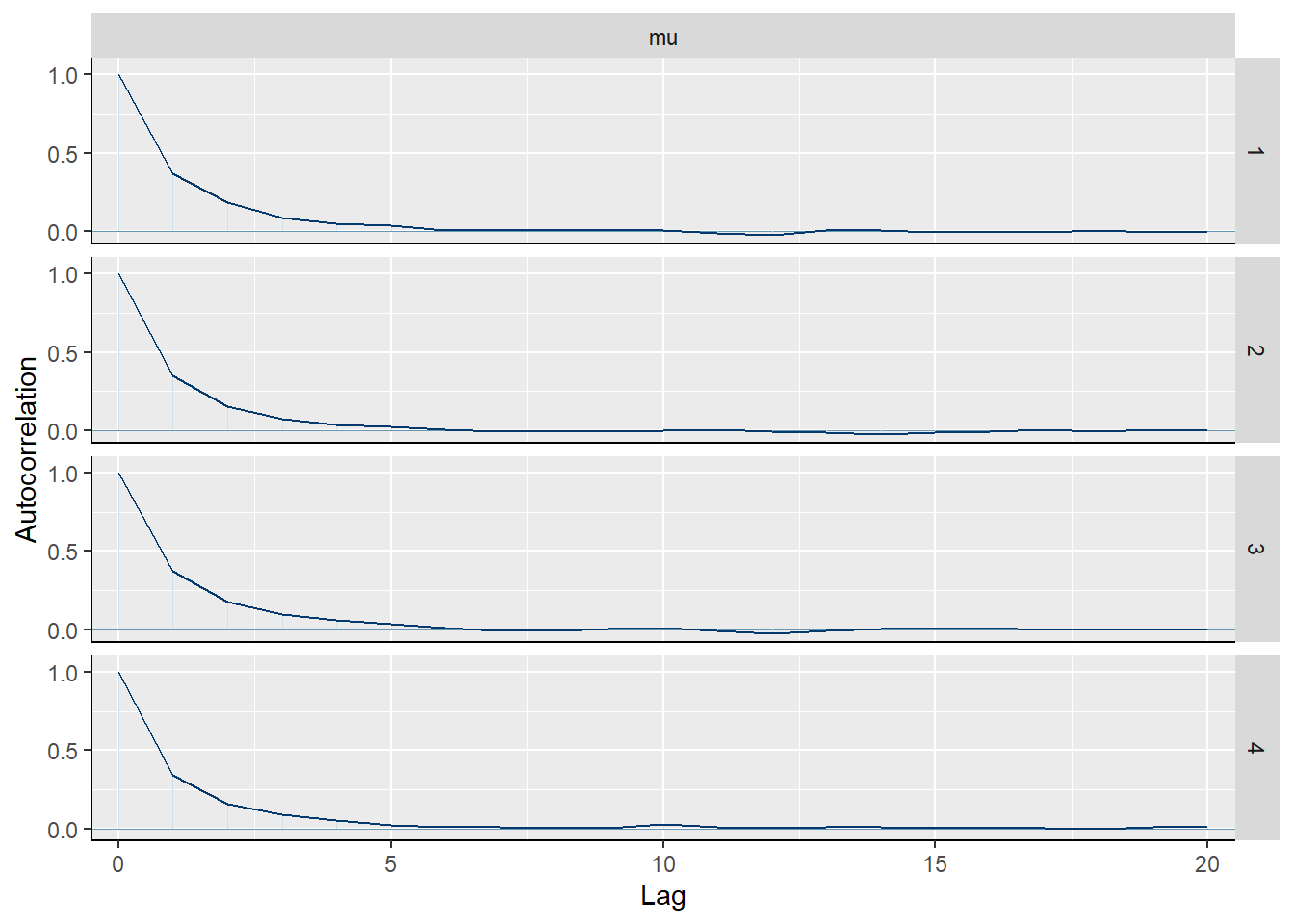
mcmc_acf(sim.MCMC.stan.Apf, pars = "sigma2")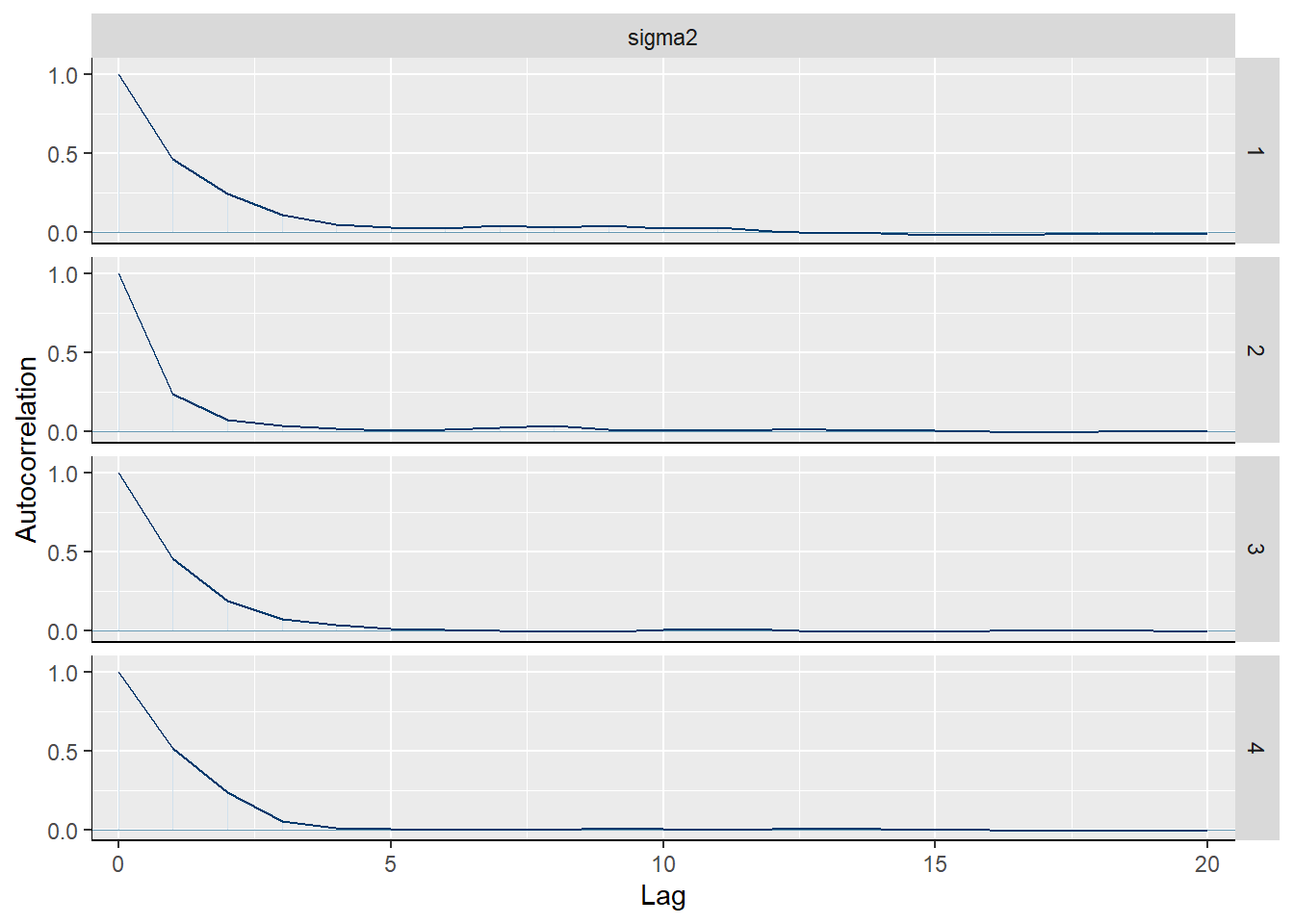
Vidimo da autokorelacijska funkcija jednako brzo opada za oba parametra kod sva 4 lanca, što sugerira dobru brzinu miješanja.
Efektivne uzoračke veličine:
- Za $\mu$: $S_{eff}=8829$
- Za $\sigma^2$: $10208$Dobivene vrijednosti sugeriraju da su aproksimacije jednako kvalitetne kao da smo koristili Monte Carlo metodu sa \(8829\) (\(10208\)) simuliranih vrijednosti za \(\mu\) (\(\sigma^2\)).
- Za \(\mu\): \(\left[1.78, 2.07\right]\)
- Za \(\sigma^2\): \(\left[0.11, 0.17\right]\)
\[P(X_{7} \in \left[1.8, 2 \right] | X_1= x_1, \dots, X_6=x_6) \approx0.51515.\]
MCMC <- rstan:: extract(sim.MCMC.stan.Apf)
ecdf(MCMC$x_tilda)(2)-ecdf(MCMC$x_tilda)(1.8)[1] 0.5451- Ovdje podrazumijevamo da nemamo apriornih informacija, odnosno da je prikladna apriorna distribucija “uniformna” (u ovom slučaju neprava za oba parametra). To jednostavno postižemo tako da ne postavimo nikakvu apriornu distribuciju u kodu (default je slabo informativna apriorna distribucija koja doprinosi efikasnom izvršenju algoritma - potiče se koristiti svoje apriorne distribucije).
modelMusiceApf2 <- "
data {
real <lower = 0> x[6]; // podaci
}
parameters {
real mu; // parametar mu
real<lower = 0> sigma2; // parametar sigma2
}
model {
x ~ normal(mu,sqrt(sigma2)); // vjerodostojnost
}
generated quantities {
real x_tilda = normal_rng(mu,sqrt(sigma2));
}
"
sim.MCMC.stan.Apf2 <-stan(
model_code = modelMusiceApf2,
data = list(x=midge$Wing.Length[Species=="Apf"]), # named list of data
chains = 4, # broj korištenih Markovljevih lanaca
warmup = 10000, # burn in period za svaki lanac
iter = 20000, # ukupan broj iteracija svakog lanca
cores = 1, # broj korištenih jezgri
refresh = 0, # no progress show
seed=934
)Usporedimo dva modela:
print(sim.MCMC.stan.Apf)Inference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 1.92 0.00 0.05 1.82 1.89 1.92 1.95 2.02 16453 1
sigma2 0.03 0.00 0.06 0.00 0.01 0.01 0.03 0.12 15596 1
x_tilda 1.92 0.00 0.17 1.58 1.83 1.92 2.01 2.26 36346 1
lp__ 6.07 0.01 1.12 3.07 5.61 6.41 6.89 7.20 11175 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:35:42 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).print(sim.MCMC.stan.Apf2)Inference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
mu 1.93 0.00 0.07 1.78 1.89 1.93 1.96 2.07 8829 1
sigma2 0.03 0.00 0.11 0.00 0.01 0.02 0.03 0.17 10208 1
x_tilda 1.93 0.00 0.20 1.54 1.83 1.93 2.02 2.31 27634 1
lp__ 5.97 0.01 1.27 2.53 5.45 6.36 6.89 7.23 7436 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:36:31 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).Ne uočavamo posebne razlike.
Zadatak 5.9 Riješite zadatak 3.5 korištenjem MCMC metode na platformi STAN.
Aproksimacija posteriornih distribucija na platformi STAN:
Paralelno ćemo napraviti 2 rješenja:
modelUsporedbaProporcija1 : (bez postavljanja apriornih distribucija, prepuštamo STAN-u odabir)
modelUsporedbaProporcija2 : (koristimo konjugirane apriorne distribucije)
modelUsporedbaProporcija1 <- "
data {
int <lower = 0, upper=60> x[3]; // podaci1
int <lower = 0, upper=60> y[3]; // podaci2
}
parameters {
real<lower = 0, upper=1> theta1; // parametar theta1
real<lower = 0, upper=1> theta2; // parametar theta2
}
model {
x ~ binomial(60,theta1); // vjerodostojnost1
y ~ binomial(60,theta2); // vjerodostojnost2
}
generated quantities {
int <lower = 0, upper=60> x_tilda = binomial_rng(60,theta1);
int <lower = 0, upper=60> y_tilda = binomial_rng(60,theta2);
}
"
podaci <- list(x=c(53,56,49), y=c(50,57,54))
sim.MCMC.stan1 <-stan(
model_code = modelUsporedbaProporcija1,
data = podaci, # named list of data
chains = 4, # broj korištenih Markovljevih lanaca
warmup = 10000, # burn in period za svaki lanac
iter = 20000, # ukupan broj iteracija svakog lanca
cores = 1, # broj korištenih jezgri
refresh = 0, # no progress show
seed=934
)
print(sim.MCMC.stan1)Inference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta1 0.87 0.00 0.02 0.82 0.86 0.87 0.89 0.92 36345 1
theta2 0.89 0.00 0.02 0.84 0.87 0.89 0.91 0.93 37397 1
x_tilda 52.42 0.02 2.97 46.00 51.00 53.00 55.00 58.00 37629 1
y_tilda 53.41 0.01 2.79 47.00 52.00 54.00 55.00 58.00 37672 1
lp__ -133.09 0.01 1.01 -135.80 -133.47 -132.79 -132.38 -132.11 18378 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:37:15 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).MCMC1 <- rstan::extract(sim.MCMC.stan1, permuted=TRUE)
###############################################
modelUsporedbaProporcija2 <- "
data {
int <lower = 0, upper=60> x[3]; // podaci1
int <lower = 0, upper=60> y[3]; // podaci2
}
parameters {
real<lower = 0, upper=1> theta1; // parametar theta1
real<lower = 0, upper=1> theta2; // parametar theta2
}
model {
x ~ binomial(60,theta1); // vjerodostojnost1
y ~ binomial(60,theta2); // vjerodostojnost2
theta1 ~ beta(12,3); // konjugirana apriorna distribucija
theta2 ~ beta(9.9875, 1.7625); // konjugirana apriorna distribucija
}
generated quantities {
int <lower = 0, upper=60> x_tilda = binomial_rng(60,theta1);
int <lower = 0, upper=60> y_tilda = binomial_rng(60,theta2);
}
"
podaci <- list(x=c(53,56,49), y=c(50,57,54))
sim.MCMC.stan1 <-stan(
model_code = modelUsporedbaProporcija2,
data = podaci, # named list of data
chains = 4, # broj korištenih Markovljevih lanaca
warmup = 10000, # burn in period za svaki lanac
iter = 20000, # ukupan broj iteracija svakog lanca
cores = 1, # broj korištenih jezgri
refresh = 0, # no progress show
seed=934
)
print(sim.MCMC.stan1)Inference for Stan model: anon_model.
4 chains, each with iter=20000; warmup=10000; thin=1;
post-warmup draws per chain=10000, total post-warmup draws=40000.
mean se_mean sd 2.5% 25% 50% 75% 97.5% n_eff Rhat
theta1 0.87 0.00 0.02 0.82 0.86 0.87 0.89 0.91 33802 1
theta2 0.89 0.00 0.02 0.84 0.88 0.89 0.91 0.93 34013 1
x_tilda 52.31 0.02 2.96 46.00 50.00 53.00 54.00 57.00 38486 1
y_tilda 53.50 0.01 2.75 48.00 52.00 54.00 55.00 58.00 38428 1
lp__ -141.44 0.01 1.01 -144.17 -141.83 -141.14 -140.73 -140.45 17213 1
Samples were drawn using NUTS(diag_e) at Mon Jun 3 09:37:58 2024.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at
convergence, Rhat=1).MCMC2 <- rstan::extract(sim.MCMC.stan1, permuted=TRUE)#Prvi model:
ecdf(MCMC1$theta1)(0.9)-ecdf(MCMC1$theta1)(0.75)[1] 0.8626ecdf(MCMC1$theta2)(0.9)-ecdf(MCMC1$theta2)(0.75)[1] 0.646075#Drugi model:
ecdf(MCMC2$theta1)(0.9)-ecdf(MCMC2$theta1)(0.75)[1] 0.88615ecdf(MCMC2$theta2)(0.9)-ecdf(MCMC2$theta2)(0.75)[1] 0.62255#Prvi model:
mean(MCMC1$theta1>MCMC1$theta2)[1] 0.31285#Drugi model:
mean(MCMC2$theta1>MCMC2$theta2)[1] 0.26895#Prvi model:
mean(MCMC1$x_tilda>55)[1] 0.146775mean(MCMC1$y_tilda>55)[1] 0.23965#Drugi model:
mean(MCMC2$x_tilda>55)[1] 0.13555mean(MCMC2$y_tilda>55)[1] 0.246325